Tangenten von Punkt A aus an K

Question

ich hänge bei dieser Aufgabe fest, wo liegt mein Rechen-/Denkfehler?

Danke :)

Answer 1

In deinem Lösungsversuch steckt weder ein Rechen- noch ein Denkfehler. Du musst lediglich noch die letzte Gleichung lösen um passende Werte für u zu finden.

Comments

ja das ist mir klar. aber ich brauche doch um eine Polynomgleichung zu lösen, ein u³; u²; u und eine Zahl?

---

Beschreibe den Gedankengang, der dich zu dieser Annahme veranlasst hat.

Außerdem, wähle in der Gleichung 0 = a·u³ + b·u² + c·u +d die Parameter a, b, c und d so, dass die Gleichung  0 = -1/2·u³ + 3/2·u² - 2 entsteht.

---

a= -1/2

b= +3/2

c= 0

d= -2

richtig?

Also wenn ich x² und eine Zahl habe -> + - Wurzel

Wenn ich x² und x habe -> Ausklammern

Wenn ich x²;x und c habe -> abc Formel

x³;x²;x und c -> Polynomgleichung mit 3 unbekannten

und immer so weiter

---

> a= -1/2
> b= +3/2
> c= 0
> d= -2

Dann bekommst du 0 = -1/2·u³ + 3/2·u² + 0·u - 2. Damit hast du ein u³; u²; u und eine Zahl; so wie du es haben wolltest.

---

Echt so einfach? Klingt logisch aber ich dachte es muss explizit von jeder Potenz eine Variable vorhanden sein..

Ok Danke, dann rechne ich mal weiter :)

---

Am einfachsten erscheint mir
0 = -1/2·u³ + 3/2·u² - 2 | *-2
u³ - 3 * u² + 4 = 0
Jetzt heißt es raten oder probieren
u = -1
ergibt schon einmal eine Lösung.
dann Polynomdivision ergibt
u = 2

Answer 2

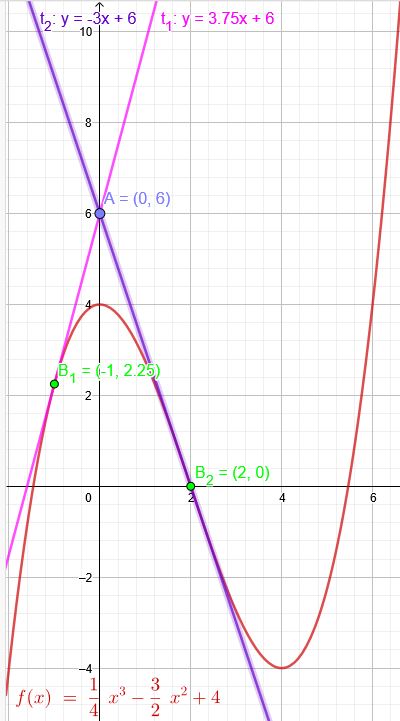
$f(x)=\frac{1}{4}x^3-\frac{3}{2}x^2+4$    A$(0|6)$

Die Berührpunkte haben die Koordinate B$(x|\frac{1}{4}x^3-\frac{3}{2}x^2+4)$

2 Punkteform einer Geraden

$\frac{y_2-y_1}{x_2-x_1}=f'(x)$

$\frac{6-\frac{1}{4}x^3+\frac{3}{2}x^2-4}{0-x}=\frac{3}{4}x^2-3x$

$2-\frac{1}{4}x^3+\frac{3}{2}x^2=-\frac{3}{4}x^3+3x^2$

$8-x^3+6x^2=-3x^3+12x^2$

$2x^3-6x^2+8=0$

$x^3-3x^2+4=0$   $x=-1$ ist eine Lösung

Polynomdivision $(x^3-3x^2+4):(x+1)=x^2-4x+4$

Somit ist $x=2$ auch noch eine Berührstelle

$B_1(-1|2,25)$  und  $B_2(2|0)$
Tangentengleichungen mit den Mitteln deiner Wahl berechnen.