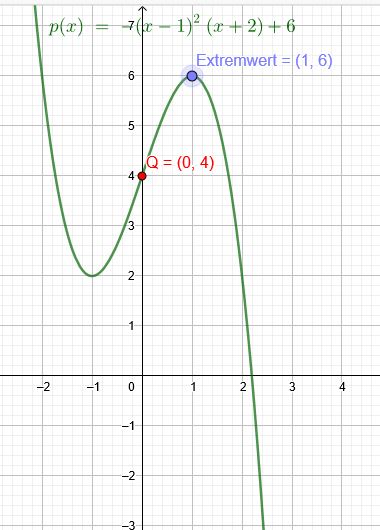
Eine ganzrationale Funktion dritten Grades hat in P \((1|6)\) eine Tangente, die parallel zur x- Achse verläuft. (Meiner Meinung nach soll das heißen, dass an diesem Punkt die Steigung 0 lautet.), und in Q \((0|4)\) einen Wendepunkt. Bestimmen Sie die Funktionsgleichung.
P \((1|6)\)↓:P´ \((1|0)\) doppelte Nullstelle:
\(f(x)=a[(x-1)^2(x-N)]\)
\(f'(x)=a[(2x-2)(x-N)+(x-1)^2 \cdot 1]\)
\(f''(x)=a[(2x-2N)+(2x-2)\cdot 1+(2x-2)]\)
Q \((0|...)\) einen Wendepunkt:
\(f''(0)=a[(-2N)+(-2)+(-2)]=a[-2N-4]=0\)
\(N=-2\):
\(f(x)=a[(x-1)^2(x+2)]\)
Q \((0|4)\) ↓ Q´ \((0|-2)\)
\(f(0)=a[(-1)^2 \cdot (2)]=2a=-2\)
\(a=-1\):
\(f(x)=-(x-1)^2(x+2)\) ↑:
\(p(x)=-(x-1)^2(x+2)+6\)