Finde die Mengen für die 2 Funktionen Mengen A,B ⊆ R, so dass die Funktion eine Umkehrfunktion besitzt.

Question

ich hänge bei einem Funktionsbeispiel fest und komm nicht weiter. Die Angabe lautet:

Finden Sie für jede der unten angegebenen Funktionen f und g zwei Mengen A,B  ⊆ R, sodass die Funktion eine Umkehrfunktion von B nach A besitzt (die Mengen A und B sollen dabei jeweils "so groß wie möglich" sein) und geben Sie die Umkehrfunktion an.

a) ƒ: A → B, x ↦ x² - 1

b) g: A → B, x ↦ x³ + 1

Ich hoffe ihr könnt mir ein paar Lösungsvorschläge machen. Danke

Comments

Hallo MatheLounge-Community,

ich sitze bei dem unten abgebildeten Beispiel fest und komme nicht mehr weiter. Besser gesagt verstehe ich nicht einmal was gefragt ist. Die Umkehrfunktion der Funktion kriege ich noch hin, aber das Finden der 2 Mengen ist etwas kompliziert. (jedenfalls für mich :D) Ich hoffe ihr könnt mir die Aufgabe erklären oder mir Tips zur Lösung dieses Beispiels mitgeben. Danke

Answer 1

Der Definitionsbereich A muss so gewählt werden, dass die Funktion injektiv ist, das heißt, dass jede Parallele zur x-Achse den Graph höchstens einmal schneiden darf. B ist die zugehörige Wertemenge.

a)   

f: ℝ₀⁺ → [ 0 ; -1 ] ;  x ↦ x² - 1     [ ℝ₀^- als Definitionsbereich ginge auch! ]

y = x² - 1

nach x auflösen:

x² = y + 1  ≥0 für y ∈  [ 0 ; -1 ] 

x = √(y+1)

Variablennamen vertauschen:

y = √(x+1)

 f ^-1(x):  [0 ; -1] → ℝ₀⁺ ;  x ↦ √(x+1)

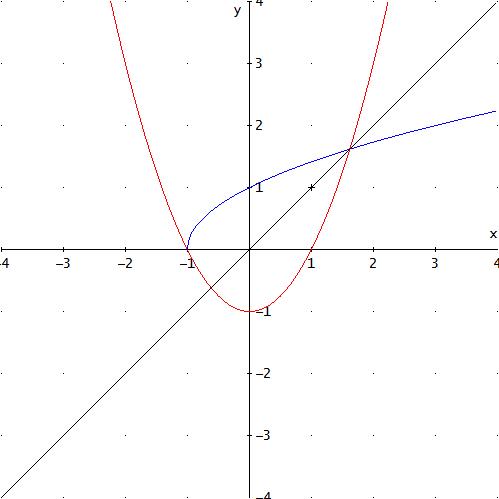
Der linke Teil der Parabel gehört für x∈ ℝ₀⁺ nicht zum Graph → f injektiv.

Der Graph der Umkehrfunktion ergibt sich durch Spiegelung an der Winkelhalbierenden y=x

b)

f: ℝ → ℝ ; x ↦ x³ +1  ist injektiv

 y = x³ +1

x³ = y -1 

x =   ³√ (y-1)    für  y≥ 1  [Radikand ≥ 0]

      - ³√ (1 -y)   für  y <1

....

Gruß Wolfgang

Comments

WOW Danke für den ausführlichen Lösungsvorschlag -Wolfgang- :D