4) Aufgrund einer linearen Preis-Absatz-Funktion werden 200 Paar Schuhe zu einem Stückpreis von 75 € abgesetzt.
Wenn man den Preis um 5€ senkt, nimmt die Absatzmenge jeweils um 50 Paar zu. Die durchnittlichen Kosten der Produktion betragen 20€
a) Bestimme die Preis-Absatz-Funktion
(200,75), (250,70)
p(x) = -5/50*(x - 200) + 75 = 95 - 0.1·x
b) Bestimme den Höchstpreis und die Sättigungsmenge
p(0) = 95
p(x) = 0
95 - 0.1·x = 0
x = 950
c) Gib den maximalen Erlös und die zugehörige Menge an
E(x) = x * p(x) = 95·x - 0.1·x^2
E(x) = 0
x = 0 und x = 950
Maximaler Erlös bei einer Menge von 950/2 = 475
E(475) = 22562.5
d) bestimme GS und GG!
K(x) = 20x
G(x) = E(x) - K(x) = 95·x - 0.1·x^2 - 20x = 75·x - 0.1·x^2 = x·(750 - x)/10
GS = 0
GG = 750
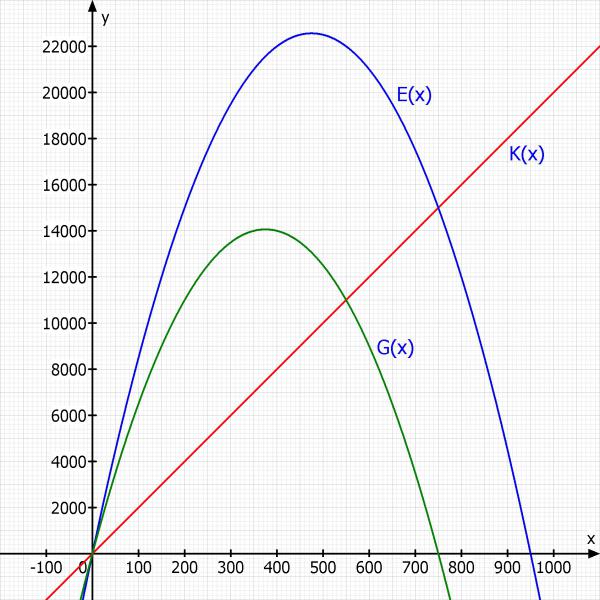
3) Zeichne die Kosten,-Erlös- Gewinnfunktionen in ein Koordiantensystem.