kann mir bitte jemand erklären, wie man das Polynom bekommt? Mit dieser Lösung komme ich nicht klar.
Aufgabe
Aufgabe
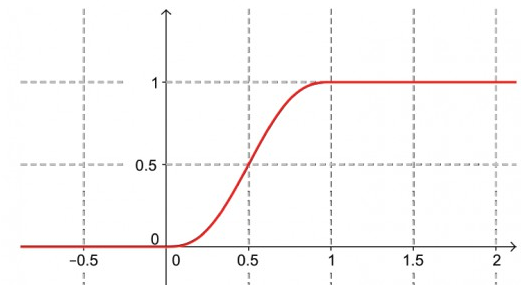
Gesucht ist eine streng mononton wachsende Funktion \( p(t) \) im Intervall \( [0,1] \) welche die konstante 0 -Funktion \( C^{2} \) -stetig auf die konstante 1 -Funktion fortsetzt. Auf diese Weise entsteht ein stetiges Schaltsignal \( u(t), \) das in der Zeit \( T=1 \) von 0 auf 1 umschaltet. Stellen Sie diese abschnittsweise definierte Funktion \( u(t) \) möglichst geschickt mithilfe der Heaviside-Funktion dar.
Lösung: Das Polynom \( p(t)=6 t^{5}-15 t^{4}+10 t^{3} \) leistet das Gewünschte. Die Heaviside-Funktion (Einheitssprungfunktion, unit jump) springt an der Stelle \( t_{0}=0 \) auf den Wert 1:
$$ H(t)=\left\{\begin{array}{ll} {0} & {t<0} \\ {1} & {t \geq 1} \end{array}\right. $$
Falls sie in einer bestimmten Software nicht vorhanden ist, kann sie oft auch relativ einfach mithilfe der meist vorhandenen Signum-Funktion definiert werden: \( H(t)=0.5 \cdot(\operatorname{sgn}(t)+1) . \) Der Funktionswert an der Stelle 0 ist dann jedoch 1/2, da sgn(0) =0.
$$ u(t)=H(t) \cdot H(1-t) \cdot p(t)+H(t-1)=\left\{\begin{array}{ll} {0} & {t \leq 0} \\ {p(t)} & {0<t<1} \\ {1} & {t \geq 1} \end{array}\right. $$