Berechnung des Flächeninhalts, der vom Funktionsgraphen und x-Achse eingeschlossen wird

Question

Berechnen Sie den Inhalt A der Fläche, die vom Graphen der Funktion f und der x-Achse über dem Intervall I eingeschlossen wird.

a) f(x) = x^4 - 5x^2 + 4  I=[-3;1]

b) f(x) = x^4 + x^3 - 3x^2 I = [-2,5;1,5]

c) f(x) = -3x^2 - 6x + 8 I=[0;3]

Answer 1

Schauen, ob f in dem Intervall eine Nullstelle hat.

Bei a) liegen die bei 2   1     -1   und  -2

Also musst du mehrere Integrale machen:

von -3 bis -2  dann von

-2 bis -1    dann von 

-1 bis  1 .

Comments

Sieht so aus
~plot~x^4-5x^2+4~plot~

Answer 2

Hallo

zua)

 

Du must dann 3 Integrale bilden und dann addieren

1. Integral:  -3 bis -2

2. Integral:  -2 bis -1

3. Integral:  -1 bis 1

Comments

Als Summe der drei Integrale erhalte ich

272/15 

Ist dies korrekt?

---

Du mußt bei dem negativen Ergebnis den Betrag nehmen ,.

ich komme auf :316/15

---

Ja das stimmt. Jetzt komme ich auch auf 316/15

---

gern

                       

:-)

---

Hallo

zu c)

  ~plot~-3x^2-6x+8~plot~

Answer 3

b)

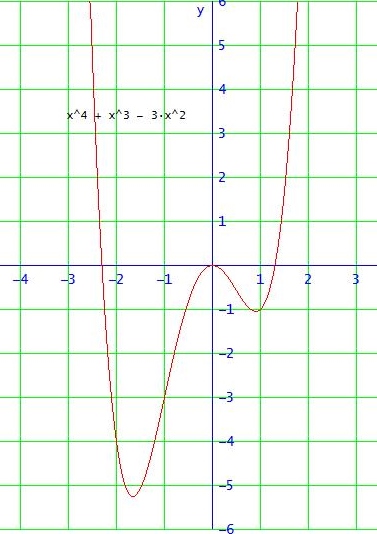
Nullstellen von f:

f(x) = x² • ( x² + x - 3 ) = 0

Nullproduktsatz  →   x₁ = 0 (doppelt)  oder  x² + x - 3 = 0

pq-Formel:  p = 1  ; q = -3 

 x_2,3 = - p/2 ± √[ (p/2)² - q ]

 x₂ ≈ -2.304   und   x₃ ≈ 1.303   (alle Nullstellen ∈ [-2,5;1,5])

wegen der doppelten Nullstelle x₁ = 0  liegt dort kein Vorzeichenwechsel vor und du erhältst die Fläche als

A = _-2,5∫^x1 f(x) dx +  |  _x1∫^x3 f(x) dx  |  + _x3∫^1,5 f(x) dx  = ........

→    A ≈ 0,431 + | -7.031 | + 0.140   →  A ≈ 7,61

Der Betrag beim zweiten Integral muss stehen, weil der Graph in diesem Intervall unterhalb der x-Achse liegt. Auch wenn über die Lage des Graphen gegenüber der x-Achse in einem Intervall Unklarheiten bestehen, kann man immer den Betrag setzen. 

Gruß Wolfgang