Tangente berechnen, wie?

Question

Durch den Punkt R sollen Tangenten an den Graphen von f gehen. Bestimmen Sie die Berührpunkte der Tangenten. 

Gegeben : -0,25x^2 + x  und R(2|2) 

Wie berechne ich die Berührpunkte von {diesen} Tangenten? Bzw. den X-Koordinaten dieser Berührungspunkte?

Answer 1

f(x) = - 0.25·x^2 + x

f'(x) = 1 - 0.5·x

Bedingung

(f(x) - 2) / (x - 2) = f'(x) --> x = 4 ∨ x = 0

t1(x) = f'(4) * (x - 4) + f(4) = 4 - x

t2(x) = f'(0) * (x - 0) + f(0) = x

Skizze

~plot~- 0.25*x^2 + x ; 4 - x ; x~plot~

Answer 2

Hier der Sachverhalt

 

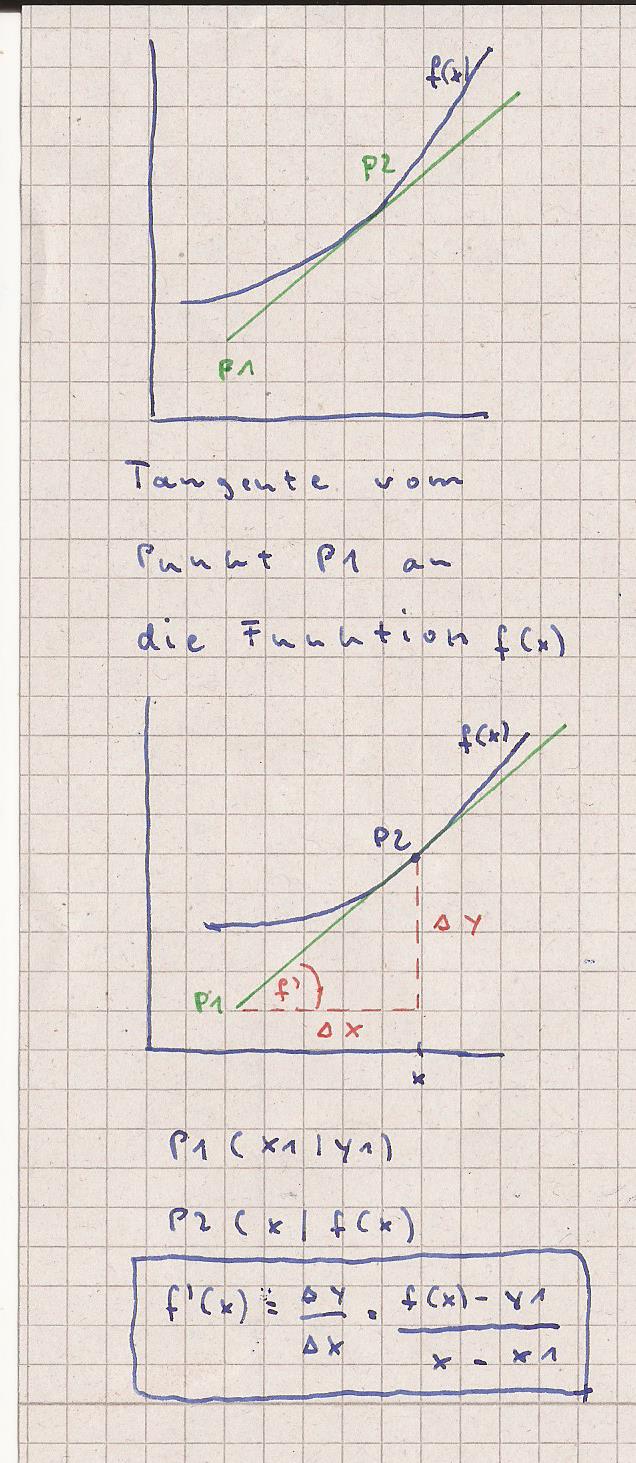
P1 ( x1 | y1 ) = ( 2 | 2 )
f ( x ) = -0.25 * x^2  + x
f ´( x ) = - 0.5 * x + 1

-0.5 * x + 1 = [ ( -0.25 * x^2 + x ) - 2 ] /  ( x - 2 )
Lösung mit abc-Formel, pq-Formel oder quadratische Ergänzung

x = 0
und
x = 4

Punkte
( 0 | f ( 0 )  ( 0 | 0 )
( 4 | f ( 4 ) ) ( 4 | 0 )

~plot~ -0,25*x^{2} +x;{2|2};x ;-x + 4 ;{0|0};{4|0} ~plot~