Berechne Berührpunkt zwischen Tangente und Logarithmusfunktion

Question

gegeben ist die Funktion: f(x)= 2ln(x)

Durch den Punkt P (0/1) verläuft eine Gerade, die Tangente an dem Graphen von f ist. Berechne den Berührpunkt und den Funktionsterm dieser Geraden.

Mein Ansatz: y=mx+t  -> 1=m*0+t -> t=1

                     mx+t = 2ln(x)

von da an weiß ich nicht mehr weiter. Blick da jemand durch?

Answer 1

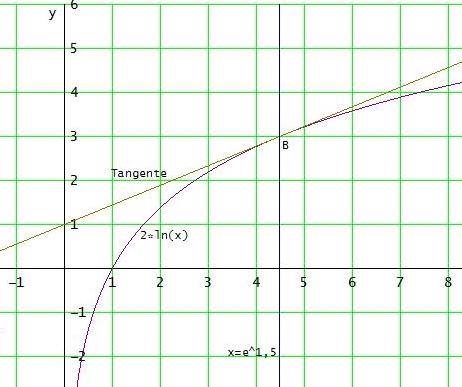
f(x)= 2ln(x) , f '(x) = 2/x  , P(0|1)

die Tangente hat eine noch nicht bekannte Berührstelle x=b, 

also einen Berührpunkt B(b | 2ln(b))

Die Steigung der Tangente ist dann f '(b) = 2/b

Die Gerade durch den Punkt P( x_p | y_p ) mit der Steigung m hat die Gleichung

y = m • ( x - x_p ) + y_p            [ Punkt-Steigungs-Formel ]   

Für die Gleichung der Tangente gilt also:

y = 2/b • (x - 0) + 1 = 2/b • x + 1

Wenn man jetzt den Berührpunkt einsetzt, erhält man eine Gleichung für b:

2•ln(b) = 2/b • b + 1  ⇔  ln(b) = 3/2 ⇔  b = e^3/2

und damit die Tangentengleichung

y = 2/e^3/2  • x + 1   ≈  y = 0,446 • x + 1

Gruß Wolfgang

Answer 2

(f(x) - 1)/(x - 0) = f'(x) --> x = e^{3/2}

t(x) = f'(e^{3/2}) * (x - e^{3/2}) + f(e^{3/2}) = 2·e^{- 3/2}·x + 1

~plot~2*ln(x);2*exp(- 3/2)*x+1;{0|1}~plot~

Answer 3

Hey Adrian!Hier musst du f(x) ableiten, wobei ln(x) abgeleitet 1/x ist. Sieh selbst