analysis f (x) = x^2 - 3x

Question

könnte  bitte  jemand  meine Ergebnisse korrigieren.

Gegeben ist die funktion: f (x) = x^2 - 3x

a) wie groß  ist die Steigung bei x= 2?

f'(2) = 1

b) Wie groß  ist  der steigungswinkel von f bei x = 2?

tan α = f'(2)

Arctan (1) = 45°

C) Unter welchem Winkel schneidet der Graph von f die y - Achse?

x= 0 --> y=0

Aber das macht kein  Sinn..

Danke

Answer 1

Hallo Samira,

a) , b)    Keine Beschwerden meinerseits :-)

c)

der Schnittwinkel zwischen Graph und y-Achse in einem bestimmten Punkt des Graphen ist per Definition der Winkel zwischen der Tangente an den Graph in diesem Punkt und der y-Achse, also zwischen zwei Geraden.

Zwischen zwei Geraden, die nicht senkrecht zueinander sind, gibt es immer zwei "Winkelmöglichkeiten", die zusammen 180° ergeben. Als Schnittwinkel ist der kleinere der beiden definiert.

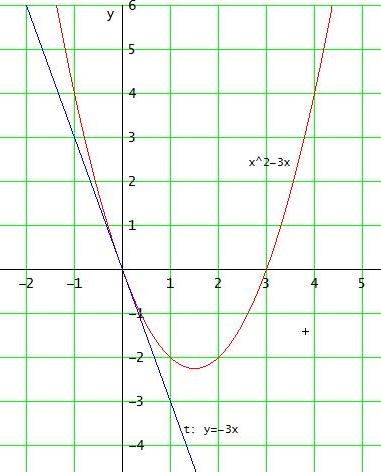
→  α_S  =  90° - | arctan( f '(0) ) | = 90° - | arctan( -3) |  = 90° - | - 71,6° |  = 18,4°

Gruß Wolfgang

Answer 2

a) und b) sind richtig

c)

90° - atan(f'(0)) = 161.6