kurvendiskussion asymptote nullstelle

Question

mit fk(x) = (e^x – k)^2, k > 0

Kann mir jemand hiervon bitte die Nullstelle, Extrempunkt und Asymptote erklären ?

Ich komme damit mit de Funktion nicht zurecht

Comments

Hi, die einzige Nullstelle ist \(x=\ln(k)\). Sie ist auch die einzige Extremstelle. Beides kann bereits am Funktionsterm abgelesen werden.

Answer 1

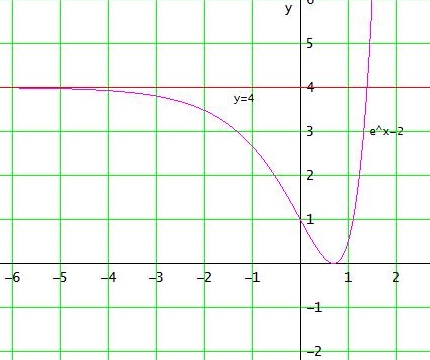
f(x) = ( e^x - k )²  mit  k>0   f(x) = 0⇔ e^x = k  ⇔  x = ln(k)  (Nullstelle)

f '(x) = 2e^x • (e^x - k) = 0    →  e^x = k   ⇔   x = ln(k)    mit VZW von  - → -+ 

  →   Tiefpunkt   T( ln(k) | 0 )

lim_{x→ - ∞}   (e^x - k)² = k²   ergibt wegen der strengen Monotonie in ] - ∞ ; ln(k) ]  

die waagrechte Asymptote  y = k²   für x → - ∞

f(x)  = (e^x - 2)²  für k = 2:

Gruß Wolfgang

Comments

wieso 2e^x *(e^x-k)

ich hätte gesagt 2(e^x-k)

---

f '(x) = 2 • (e^x - k) • e^x    (innere Ableitung bei der Kettenregel)

---

Könnten sie mir bitte die Kettenregel erklären ...Ich verstehe das nicht

---

Kurzfassung der Kettenregel:   [ f(u)] ' = f '(u) • u'      ( u = g(x) )

Kettenregel für diesen Fall:

 [ x² ] ' = 2x

ist u ein Term mit x  →  [ u² ] '  = 2u • u'   (innere Ableitung)   

mit u = e^x - k →    [ (e^x - k)² ] ' = 2 • (e^x - k) • e^x

Answer 2

Nullstelle: Löse die Gleichung 0 = (e^x – k)² nach x auf

Extrempunkte: f_k'(x) = 2(e^x - k)·e^x . Löse die Gleichung 0 = 2(e^x - k)·e^x nach x auf um Kandidaten für die Extrempunkte zu finden. Ziehe eine hinreichnde Bedingung heran um zu überprüfen bei welchen der Kandidaten es sich tatsächlich um Extremstellen handelt.

Asymptote: k² für x→ -∞, ∞ für x→ ∞

Comments

∞ als Asymptote erscheint mir etwas gewöhnungsbedürftig :-)

Answer 3

mit fk(x) = (e^x – k)², k > 0

Beim Extrempunkt mußt Du noch den y- Wert ermitteln und den Nachweis für den Extrempunkt erbringen.