Verteilung der Wahrscheinlichkeiten

Question

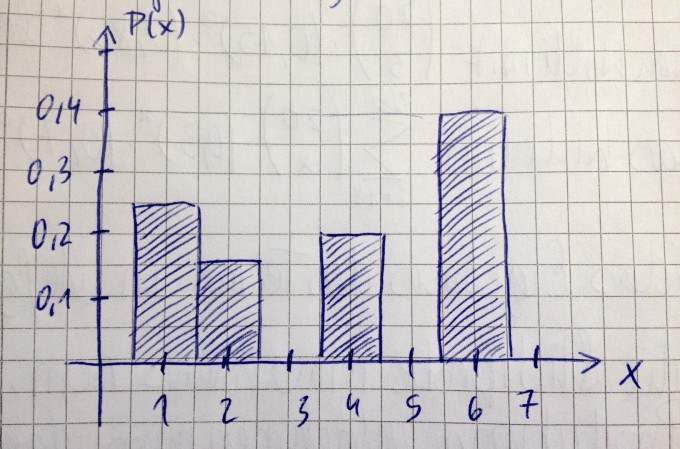
Hier ist die Verteilung der Wahrscheinlichkeiten für das Auftreten von Augenzahlen beim Würfel eines "gezinkten" Würfels dargestellt. Der Würfel hat keine Augenzahl 3 und keine Augenzahl 5. Dafür sind die Augenzahlen 1 und 6 doppelt. Die Massenverteilung des Würfels dürfte auch nicht ganz gleichmäßig sein.

a) Begründen Sie, warum es sich bei der graphischen Darstellung tatsächlich um eine Wahrscheinlichkeitsfunktion handelt. ( Bild ist im Anhang)

b)Berechnen Sie den Erwartungswert und die Standardabweichung für diesen Zufallsversuch.

c) Angenommen mit dem oben beschriebenen Würfel wird folgendes Glücksspiel veranstaltet: Bei einer Augenzahl unter drei muss der Spieler 4 EURO bezahlen, bei einer 3,4 oder 5 erhält er nichts, bei einer sechs erhält er 20 EURO. Berechnen Sie für dieses Spiel einen fairen Einsatz.

Answer 1

a) Es handelt sich um eine Wahrscheinlichkitsfunktion weil

• P(x) ≥ 0 für alle x
• P(1) + P(2) + P(3) + P(4) + P(5) + P(6) = 1
  

b)

• Erwartungswert ist E = 1·P(1) + 2·P(2) + 3·P(3) + 4·P(4) + 5·P(5) + 6·P(6)
• Standardabweichung ist σ = √[(E-1)²·P(1) + (E-2)²·P(2) + (E-3)²·P(3) + (E-4)²·P(4) + (E-5)²·P(5) + (E-6)²·P(6)]

c) Erwartungswert für das Spiel ist E = -4·(P(1)+P(2)) + 20·P(6). Die Gegenzahl dieses Erwartungswertes ist ein fairer Einsatz.