Gebrochenrationale Funktionen (Asymptoten)

Question

Hallo

Gib anhand der Funktionen die Gleichungen der Asymptoten an und skizziere den Graphen mit Hilfe der Asymptoten sowie einiger geeigneter Funktionswerte

A) f: x-> x/x-2

    Asymptoten: x= ?     y= ? 

     f(1)= ?   ; f (?)= ?

? Bedeutet leeres Kästchen

B) f: x->3/x*(x+2)

Asymptoten: x= ? y= ?

f(-3)=?   ; f(?)= ?

Wie gehe ich vor und wie muss ich zeichnen?

Comments

Achtung: Es gilt Punkt- vor Strichrechnung, wenn du keine Klammern setzt.

Bsp. x/x-2 = 1-2 = -1  (?)

Bitte Eingabe nochmals kontrollieren.

https://www.wolframalpha.com/input/?i=x%2Fx-2

---

f: x-> x/x-2

heißt sicherlich

f ( x ) = x / ( x - 2 )

Polstelle
x -2 = 0
x = 2 ( Asymptote )

Polynomdivision
x : ( x - 2 ) = 1  - 2 / ( x - 2 )

lim x −> - ∞ = 1
lim x −> + ∞ = 1

~plot~ x / ( x - 2 ) ; 1 ; x = 2 ~plot~

Asymptoten
x = 2
y = 1

Answer 1

A)

bei  senkrechten Asymptoten  der Form x = ?  ist  ? eine Zahl x₀ bei der  ein Nenner = 0  wird (Definitionslücken), falls der zugehörige Faktor x-x₀ im Nenner sich nicht wegkürzen lässt

→  x / (x-2)   hat die senkrechte Asymptote  x = 2

Um die Asymptote der Form y = ? zu erhalten, musst du Zähler durch Nenner dividieren (Polynomdivision).

   x    : (x-2) =  1 + 2 / (x-2)         y = 1     (der Rest strebt gegen 0 für  x→ ∞)

-(x-2)

-------

      2

Die Asymptote ist dann der ganzrationale Anteil    y = 1 des Ergebnisses.

(der Rest strebt gegen 0 für  x→ ∞)

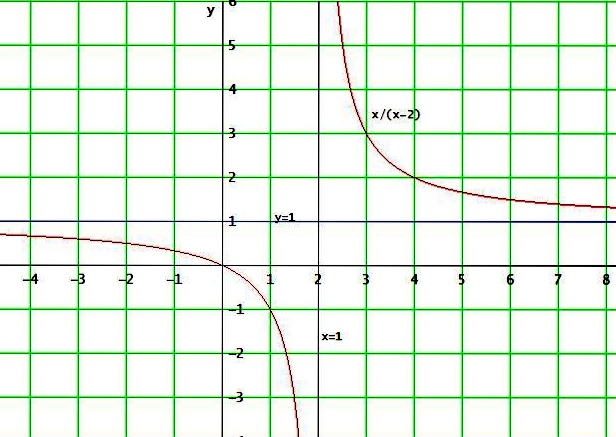
Es muss im Bild x=2 (statt x=1) heißen

B) 

 Hier erhältst du zwei senkrechte Asymptoten x = ....... ??

 und eine waagrechte Asymptote  y = 0, weil sich der Funktionswert  für x→∞ dem Wert 0 beliebig nähert.

Gruß Wolfgang