Die Brücke sieht irgendwie so aus - natürlich symmetrisch; bin kein großer Zeichner :-)
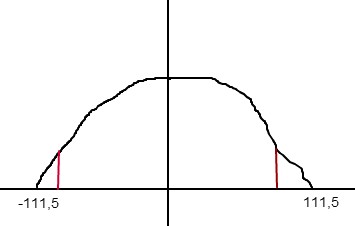
Wir haben also eine Parabel mit
f(-111,5) = 0
f(111,5) = 0
f(111,5 - 1,2) = f(110,3) = 2
Die Parabel lässt sich allgemein beschreiben als
f(x) = ax^2 + bx + c
Wir setzen ein:
f(-111,5) = a (-111,5)^2 + b (-111,5) + c = 0, also 12432,25 a - 111,5 b + c = 0
f(111,5) = a (111,5)^2 + b (111,5) + c = 0, also 12432,25 a + 111,5 b + c = 0
f(110,3) = a (110,3)^2 + b (110,3) + c = 2, also 12166,09 a + 110,3 b + c = 2
Daraus folgt
a = -0,0075142771
b = 0
c = 93,4193718064
Damit wird die parabelförmige Brücke beschrieben durch
f(x) = -0,0075142771x^2 + 93,4193718064
Setzen wir x = 0 (denn die höchste Stelle der Brücke ist auf der y-Achse), so erhalten wir eine maximale
Höhe von 93,4193718064m
b)
Den Teil versuchst Du bitte selbst - Verfahren wie oben, es ändert sich nur die 3. Gleichung in
f(110,3) = 1,9