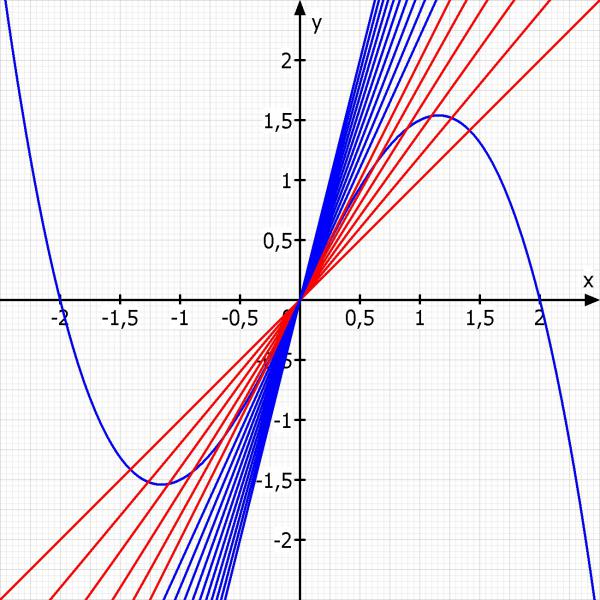
Schnittpunkte bestimmt man über ein Gleichsetzen der Funktionen
f(x) = g(x)
- 0.5x^3 + 2x = mx
0.5x^3 + mx - 2x = 0
x(0.5x^2 + m - 2) = 0
Wegen dem Nullprodukt ist die Gleichung für x = 0 immer erfüllt. Damit wir keine weitere Lösung haben darf die Klammer nie Null werden.
0.5x^2 + m - 2 = 0
0.5x^2 = 2 - m
x^2 = 4 - 2m
x = ± √(4 - 2m)
Das ist nicht Lösbar, wenn die Diskriminante < 0 ist.
4 - 2m < 0
2m > 4
m > 2
Für m = 0 ist allerdings auch die Lösung in der Klammer x = 0 daher kann man m = 2 auch noch wählen.
Für m ≥ 2 gibt es hier also keine weiteren Schnittpunkte. Ich zeichne das mal