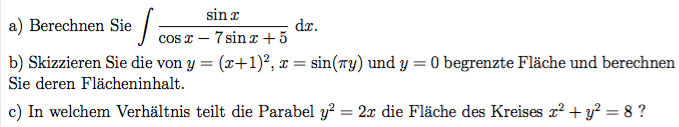
Also ich habe leider folgendes Problem schon bei der a) und zwar komme ich nicht auf das richtige Ergebnis. Ich habe das mittels nachträglicher Differenzierung geprüft wo eigentlich dann wieder die Ausgangsfunktion herauskommen sollte. Kann mir mal einer die Herangehensweise zeigen, denn irgendwo scheint mir ein Fehler unterlaufen zu sein. Denn meine Lösung stimmt auf nach mehrmaligen ausprobieren nicht.
Bei der b habe ich das selbe Problem. Grundsätzlich ist die Herangehensweise klar. Man bestimmt die eingeschlossene Fläche mittels Integral. Die Lösung sollte dann der Flächeninhalt sein. Mein Ergebnis ist aber leider viel zu groß.
Bei c habe ich zuerst die beiden einzelnen Flächen wiederum über Integration bestimmt, und um ein Verhältnis zu erhalten die beiden durcheinander geteilt. Das Ergebnis ist zwar einigermaßen sinnig aber nach dem Zeichen der beiden Funktion ist schon optisch zu sehen, dass das Ergebnis nicht stimmen kann.
Ich danke euch schon vielmals für eure Hilfe Irgendwie ist heute der Wurm drin.