Question

Bestimmen Sie die Punkte vom Graphen der Funktion f : [2; -2] -> R; f(x) = x^2-(3/2), deren Entfernung zum Ursprung minimal ist.

Also, fast die ganze Aufgabe schon oben genannt ist, es gibt noch eine Kleinigkeit:
Fertigen Sie zunächst eine Skizze des Problems an.

Meine Probleme ist: Ich verstehe die Aufgabe ihrgenwie nicht. Ich habe ein Punkt (2;-2), muss ich der x-Wert für dem ausrechnen und dann die xn+1, xn-1 ausrechnen, oder vertehe ich diese ganz falsch?

Wenn es geht die Rechenweg mir Erklärungen wird auch ganz gut passen. Aber ich glaube wenn ich die Aufgabe verstehen werde, kann ich die schaffen. Nur zum Vergleich das andere.

Danke für ihre Aufmerksamkeit.

Answer 1

Dein Problem lässt sich graphisch in etwa so darstellen: 

 

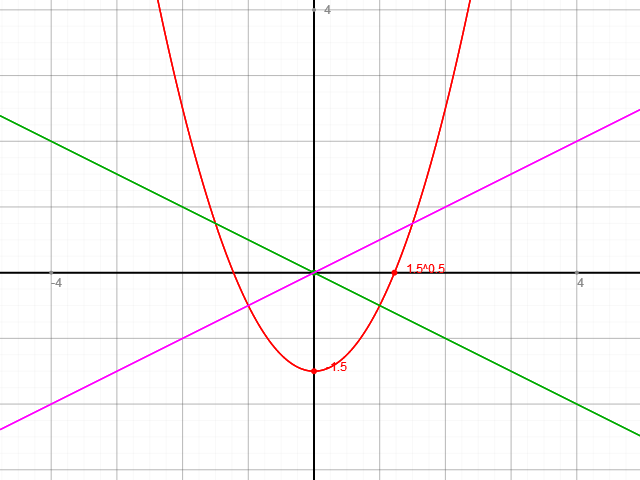
Die Funktion f(x) = x^2 - 3/2 ist die rote Parabel, und die Schnittpunkte mit der grünen bzw. der violetten Gerade sind die Punkte des Graphen von f(x), die vom Ursprung den geringsten Abstand haben. 

Das Ganze läuft mal wieder auf Pythagoras hinaus: 

Gehen wir auf der x-Achse (in dieser Skizze) eine Einheit nach rechts, haben wir eine Kathete, und dann nach unten zum Schnittpunkt, haben wir die 2. Kathete eines rechtwinkligen Dreiecks, dessen Hyotenuse die grüne Strecke vom Ursprung bis zum Schnittpunkt ist. Diese soll minimiert werden. 

Also: 

d = √(x^2 + |f(x)^2|)

d = √(x^2 + |(x^2 - 3/2)^2|)

d = √(x^2 + x^4 - 3x^2 + 9/4)

d = √(x^4 - 2x^2 + 9/4)

d wird minimal, wenn d^2 minimal wird.

d^2(x) = x^4 - 2x^2 + 9/4

d^2'(x) = 3x^3 - 4x = x * (3x^2 - 4)

Das muss = 0 gesetzt werden:

3x^2 = 4

x^2 = 4/3

x1 = √(4/3) ≈ 1,15

x2 = -√(4/3) ≈ -1,15