Approximation der Binomialverteilung durch die Gaußsche Normalverteilung

Question

ALSO :D 

Wie schon gesagt handelt es sich bei meinem Problem um die Approximation der Binomialverteilung durch die Gaußsche Normalverteilung ...

und zwar habe ich die Normal Formel benutzt  

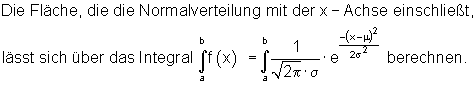
habe für b= 200

a= 0

sigma= 8,9653

sigma^2 = 80.376

Erwartungswert = 119,5 

Nun bekomme ich allerdings als Ergebnis : 2,99419983

Das kann doch nicht sein oder?  Müsste der Wert nicht kleiner 1 sein?   

Und wenn nicht WARUM IST DAS SO ?   und wie gehe ich damit um ? 

Die Frage ist nämlich : berechnen sie die Wahrscheinlichkeit, dass es in 365 Tagen höchstens 200 mal regnet mit der Tagesregenwahrscheinlichkeit von 239/730 

Answer 1

Du solltest hier 1 heraus bekommen. weil das was du ausrechnest weit über den 3 sigma bereich hinaus geht.

Comments

OK 1 finde ich super :D und könntest du mir erklären wie ich dass dann rechnen muss? :)  bzw. wie ich das erkläre ?

---

Rein rechnerisch

P(0 ≤ x ≤ 200) = Φ((200.5 - 119.5)/8.965) - Φ((-0.5 - 119.5)/8.965) = Φ(9.04) - Φ(-13.39) = Φ(9.04) - (1 - Φ(13.39)) = 1 - (1 - 1) = 1

Aber der 3 Sigma bereich ist das Intervall

[119.5 - 3·8.965; 119.5 + 3·8.965] = [93; 146]

Die Wahrscheinlichkeit für 93 bis 146 Regentage sollte also vermutlisch schon an die 99% ergeben. Wenn ich diesen Bereich noch weiter vergrößer komme ich unendlich dicht an die 100% heran.

---

OH DANKE DANKE DANKE !!!!!  

magst du mir nur noch verraten wie die Formel heißt mit der du das eben vorgerechnet hast ? :) 

Du hast mich echt gerettet !

---

Grundsätzlich die Sigmaregeln und die Formel für die normierte Normalverteilung.

---

Ok klingt jetzt vlt. doof aber wie hast du groß Phi ausgerechnet von z.B. 9.04 ?  

---

Groß Phi schlägt man nach Dabei darfst du wissen das alles Φ(z) für z >= 4 sowieso mit 1 angenähert werden kann.

---

Oh supi das mit dem größer gleich 4 wusste ich nicht :)

Ich kann es nur wieder sagen du rettest mich :D

---

Bis wohin geht deine Tabelle von Φ ? Meine geht irgendwie bis 3.79. Alles ab da tu ich einfach so als wäre es 1.

Ist ja eh nur eine Näherung und kann bei bedarf auf anderem Wege genauer gerechnet werden.

---

bis 4.09  und da tut sich am ende auch nicht mehr so wirklich was :D linkhttp://massmatics.de/merkzettel/#!911:Tabelle_Standardnormalverteilung

Nun aber meine letzte Frage :D

Wenn ich für Φ(-2,2308) habe, dann mache ich da doch einfach 1-(Φ(2.2308)) draus oder? 

P.s. die Abinote widme ich dir :D

---

Wenn ich für Φ(-2,2308) habe, dann mache ich da doch einfach 1-(Φ(2.2308)) draus oder? 

Richtig.

Dieses Jahr haben meine Schüler die ich im mündlichen Abi hatte alle besonders gut abgeschnitten. Das mag allerdings daran liegen das das mündliche Abi dieses Jahr nicht so schwer war.

Die schriftlichen Abiturienten haben allerdings dieses Jahr etwas schlechter abgeschnitten als letztes Jahr. Das kann ein Hinweis darauf sein, dass das schriftliche Abi etwas schwerer war.

---

Ja ich hab meine mündliche morgen vor mir und bei mir an der Schule liefen die mündlichen Prüfungen bis jetzt nicht so wirklich gut... Meine Prüferin hat bis jetzt als beste Note 6 Punkte verteilt :D   

Ich hoffe mal, dass ich nicht so abschneide ...  Aber wird schon :D 

---

Meine schlechteste Schülerin hat dieses Jahr mit 8 Punkten im mündlichen Abi abgeschnitten. Allerdings weil sie in der Fragerunde wohl recht schlecht war.

---

:D na dann bleibt ja noch Hoffnung :)

---

Ich drück dir auf jeden Fall die Daumen und Wünsche viel Erfolg.