Norm konvergenz einer Folge

Question

Ich habe die drei Normen:

 

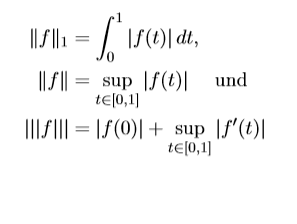
Ich soll nun zeigen, dass eine konvergente Folge,die bezüglich der zweiten Norm || · || konvergiert, auch bzgl ||·||₁ konvergiert und dass eine konvergente Folge, die bezüglich der dritten Norm |||·||| konvergiert, auch bzgl der zweiten Norm konvergiert.

Also quasi von unten nach oben.

Ich versuche mal anzufangen:
Ich nehme mir eine Folge a_n und sage,dass diese in der zweiten Norm konvergiert, also

limes n -> unendlich von sup | f_n(t) -f(t) | = 0

Jetzt nehme ich die erste Norm und möchte zeigen:

limes n -> unendlich von ( ∫  von 0 bis 1 von ( | f_n(t) -f(t) | ) dt = 0  )

Kann ich aus der ersten Aussage schließen, dass | f_n(t) -f(t) | gegen 0 läuft für n gegen unendlich? Das supremum gibt ja den größten Abstand( muss nicht in der Menge enthalten sein) an. Damit dieser Zustande kommt, muss aber doch bereits  | f_n(t) -f(t) | -> 0 gelten oder nicht?

Dann würde der Integrand gegen 0 laufen und somit würde die Folge auch bezüglich der ersten Norm konvergieren.

Zu 3. => 2. 

Konvergiert eine Folge bezüglich dieser Norm,so ist:
limes n-> unendlich =  | f_n(0) -f(0) | + sup | f'_n (t) - f(t) | = 0

Da beide Summanden positiv sind, müssen sie jeweils gegen 0 laufen.

| f_n(0) -f(0) | sagt aus, dass die Funktion im Nullpunkt "übereinstimmt" mit der Funktionenfolge.

sup | f'_n (t) - f(t) | sagt nun aus, dass die Steigung in jedem Punkt "übereinstimmt"

Darauf sollte man doch schließen können , dass  | f_n(t) -f(t) | -> 0 gilt oder nicht?

Wie drücke ich das mathematischer aus?

Ich hoffe jemand kann meinem Gedankengang folgen.

Liebe Grüße,
Marvin

Answer 1

Hi,
es gilt
$$ \int_0^1 |f(t)| dt \le \int_0^1 \sup_{t\in [0,1]} |f(t)|\ dt = \sup_{t\in [0,1]} |f(t)| $$ Daraus folgt die erste Aussage

Weiter gilt
$$ | f(t) | \le | f(t) - f(0) | + | f(0) | = \left|  \int_0^t f'(s)\ ds \right| + | f(0)| \le $$ $$ \int_0^t \left| f'(s) \right|\ ds + | f(0)| \le $$
$$ \int_0^1 \sup_{s \in [0,1]} \left| f'(s) \right|\ ds + | f(0)| \le \sup_{t \in [0,1]} \left| f'(t) \right| + | f(0)|  $$ und daraus folgt
$$ \sup_{t\in [0,1]} |f(t)| \le \left| f'(t) \right| + | f(0)| $$ und daraus folgt die zweite Aussage.