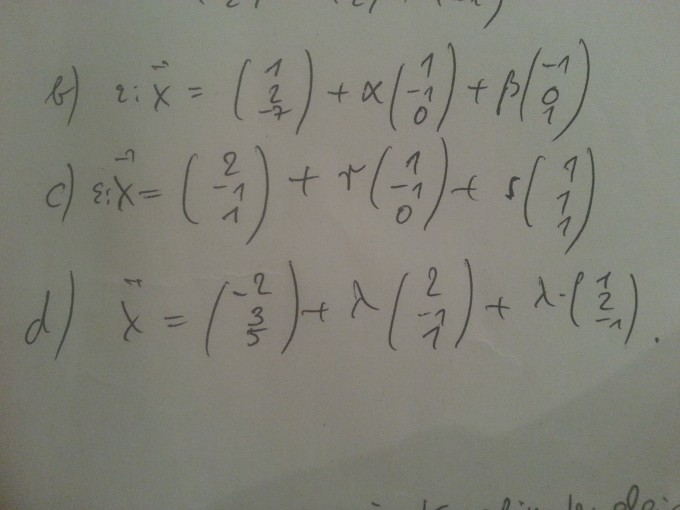Normalengleichung mithilfe Normalenvektor bestimmen

Question

ich versuche verzweifelt aufgabe c und d zu lösen, aber schaffe es nicht. Man soll erst den Normalenvektor herausfinden und dann die Normalengleichung bestimmen. Kann mir jemand bei dem herausfinden des normalenvektors helfen?

Mein ansatz z.b zu aufgabe c: 

(n1|n2|n3)*(1|-1|0)=0

(n1|n2|n3)*(1|1|1)=0

1: 1n1-1n2-0n3

2: 1n1+1n2+1n3 

Untergeordnetes gleichungssysten => 3variabeln, 2gleichungen also eine variabel frei..  n1=t

Aus 2 ergibt sich demnach:

t+1n2+1n3

Ab hier komme ich nicht mehr weiter und bei aufgabe d gar nicht mehr.. wie kann ich das nach n3 auflösen? Sodass da steht sowas wie 2 t=n3 steht... bitte um hilfe

Answer 1

1: 1n1-1n2-0n3

2: 1n1+1n2+1n3 

Untergeordnetes gleichungssysten => 3variabeln, 2gleichungen also eine variabel frei..  n1=t

Aus 2 ergibt sich demnach:

t+1n2+1n3  und aus 1 gibt es  n1 = n2 also auch n2=t

dann

t + t + n3 = 0

n3 = -2t also Normalenvektior

( t ; t ; -2t ) z.B.  ( 1 ; 1 ; -2 )

Probe passt!

Answer 2

ein Normalenvektor \(\vec{n}\) ergibt sich jeweils direkt als Keuzprodukt (Vektorprodukt) der beiden Richtungsvektoren, die bei den Parametern stehen.

Mit dem Stützvektor (Aufpunkt)  \(\vec{a}\), der in den gegeben Ebenengleichungen jeweils vorn ohne Parameter steht, ergibt sich dann die Normalengleichung aus

\(\vec{n}\) • \(\vec{x}\) - \(\vec{n}\) • \(\vec{a}\) = 0

----------

So wie d) dasteht, ist es wegen der gleichen Parameter eine "ungeordnete" Geradengleichung.

Gruß Wolfgang