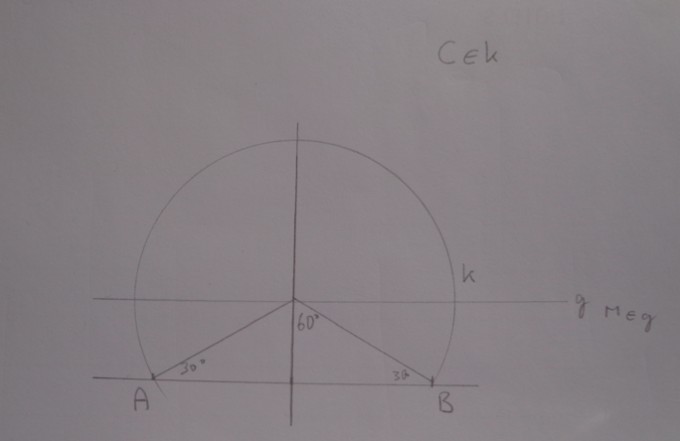
Wenn ich (oben) mit dem Fasskreis über AB beginne und g im Abstand 2 cm von c einzeichne, könnte der Inkreismittelpunkt zufälligerweise gerade oder beinahe (Zeichenungenauigkeit berücksichtigen!) im Fasskreismittelpunkt liegen.
Man könnte einfach mal vermuten, dass er dort ist , ihn zeichnen und dann die Tangenten anlegen. --> C. (Resultiert ein gleichseitiges Dreieck?) Das ist nun aber keine richtige Konstruktion.
Bekannt ist nur, dass C auf k und M auf g liegen. Aber wo?
Anfang in der Ecke C (Vorschlag Mathecoach) gibt bei mir Folgendes:

Die ausgezogenen Linien sind ± genau konstruiert. Die gestrichelte Linie ist von Auge eingepasst (Konstruktionsidee an dieser Stelle fehlt mir auch) und gemessen ziemlich genau 7cm lang. Sie steht recht genau senkrecht auf der Winkelhalbierenden. Auch hier resultiert (in Konstruktionsgenauigkeit) ein (beinahe?) gleichseitiges Dreieck.
Vielleicht sollte man mal nachrechnen, wie gross der Inkreisradius bei einem gleichseitigen Dreieck mit Seitenlänge 7 cm ist.
Zu einer richtigen Konstruktion (falls überhaupt möglich) braucht es aber bei beiden Ansätzen noch eine zündende Idee.
Daher von mir aus erst mal Fragen an den Fragesteller: Hast du exakt abgeschrieben. Sind wirklich gamma=γ und c und der Inkreisradius rho =ρ gegeben? Welche Klassenstufe besuchst du und welches Thema behandelt ihr denn zur Zeit?
