Schulgebäude: Schulbus hält an den Punkten (0|0) und (0|-5). Graphen und Ufer zuordnen ...

Question

EDIT: Ursprüngliche Überschrift "Integralrechnung - Schwere Aufgabe" mit Tags: integral anwendung ausrechnen berechnen integralrechnung graph . 

!

Ich komme leider bei einigen Aufgaben nicht weiter. Die Aufgaben a) und b) habe ich bereits gelöst. Bei den restlichen komme ich leider nicht weiter. Koordinatensystem und Aufgaben, sind auf dem Bild zu sehen. Hilfe wäre super!

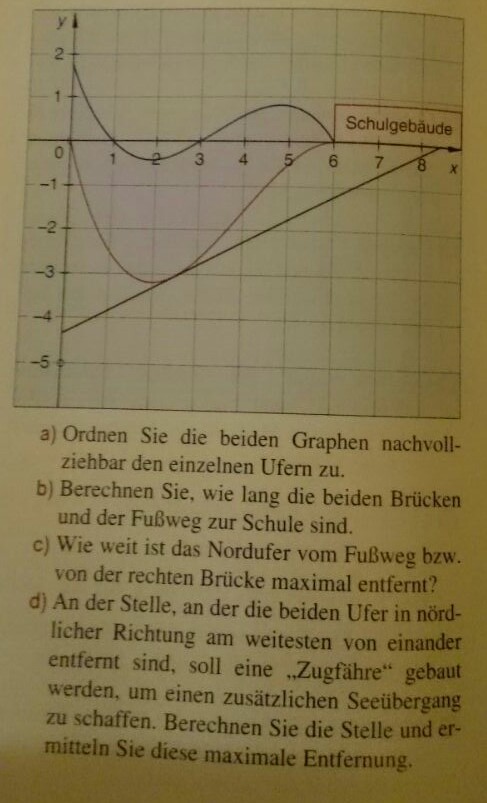
Ausgangssituation: Ein Berufskolleg bezieht ein neues Schulgebäude außerhalb des Stadtkerns auf einem Gelände, das an einem See liegt, dessen Ufer durch die Graphen der reellen Funktionen f(x)=-0,1x³ + x² - 2,7x + 1,8 und g(x)=-0,1x³ + 1,2x² - 3,6x begrenzt wird. Die Zugangsstraße verläuft entlang der negativen y-Achse, der Fußweg zur Schule teilweise über Brücken entlang der x-Achse. Der Schulbus hält an den Punkten (0|0) und (0|-5).

Comments

Bisher hat das ganze absolut nichts mit Integralrechnung zu tun. Es ist klar, dass du diese Aufgabe als besonders schwer empfindest, wenn du vermutlich nicht mal die Fragen verstanden hast. Du musst dir ganz genau klar machen was in den Fragen überhaupt gefragt wird und wie du es erstmal ohne zu rechnen nur anhand der Zeichnung beantworten könntest. Näherungsweise kannst du alle Antworten bereits aus der Zeichnung ablesen. Damit diese etwas genauer werden verwendet man die Rechnungen.

Answer 1

a)

Zuordnung über y-Achsenabschnitt. Die obere Funktion ist die Funktion f die untere die Funktion g.

b)

Nullstellen f(x) = 0 --> x = 6 ∨ x = 3 ∨ x = 1

Die Brücken überspannen den Fluss auf 1 LE und auf 3 LE.

Der Fußweg zur Schule beträgt vom Punkt (0 | 0) aus 6 LE

c)

Extrempunkt f'(x) = 0 --> x = 4.786

f(4.786) = 0.8209 LE

d)

d(x) = f(x) - g(x) = (- 0.1·x^3 + x^2 - 2.7·x + 1.8) - (- 0.1·x^3 + 1.2·x^2 - 3.6·x) =

d(x) = - 0.2·x^2 + 0.9·x + 1.8

d'(x) = 0.9 - 0.4·x

Extremwerte d'(x) = 0 --> x = 2.25

d(2.25) = 2.813 LE