Heute werde ich erklären was Dreieckszahlen sind.
Wenn man das Wort hört, dann denkt man an Zahlen die einen Dreieck bilden können. Das ist auch richtig. Wenn man Zahlen (z.B 1 bis 4) durch Punkte ersetzt und daraus ein Dreieck formen kann, dann ist es eine Dreieckszahl. Das klingt erstmals komisch und verwirrend, doch so schwer ist es nicht.
Um das zu verstehen muss man Vorwissen haben.

Carl Friedrich Gauß (siehe Bild) musste im Mathe-unterricht die Zahlen von 1 bis 100 addieren. Nach wenigen Minuten war er fertig. Er hat nämlich die erste und letzte Zahl zusammengezählt, die zweite und die vorletzte usw. das Ergebnis war immer gleich.1+100=101
2+99=101
3+98=101usw.
Man kann es auch zusammenfassen: 50*101=5050 fertig
Was hat das jetzt mit Dreieckszahlen zu tun?
Für die Addition natürlicher Zahlen gibt es eine Formel.
$$ \frac { n*(n+1) }{ 2 } $$
Genau diese Formel benutzt man auch, wenn man Dreieckszahlen berechnen will.
Eine Dreieckszahl wäre z.B 10,
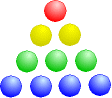
denn 10 Punkte oder Zahlen von 1 bis 10 ergeben ein Dreieck.
$$ \frac { n*(n+1) }{ 2 } $$
Wenn man für n eine Zahl einsetzt, z.B 17 und es ausrechnet, dann kommt die Dreieckszahl raus:
$$ \frac { n*(n+1) }{ 2 } \\ \\ =\frac { 17*(17+1) }{ 2 } \\ \\ =\frac { 17*18 }{ 2 } \\ \\ =\frac { 306 }{ 2 } \\ \\ =153 $$
n ist die Grundseite des Dreiecks (im Falle des Bildes n=4) weil 4 Punkte ganz unten sind.
5050 ist auch eine Dreieckszahl, denn:
$$ \frac { n*(n+1) }{ 2 } \\ \\ =\frac { 100*(100+1) }{ 2 } \\ \\ =\frac { 100*101 }{ 2 } \\ \\ =\frac { 10100 }{ 2 } \\ \\ =5050 $$
Man kann auch sagen:
Die Summen natürlicher Zahlen ergeben eine Dreieckszahl z.B 1 bis 4 : 1+2+3+4=3+7=10 Damit ist 10 eine Dreieckszahl. oder auch z.B 1-12. Diese Zahlen befinden sich auf der unteren Grundseite des Dreiecks.
Die ersten Dreieckszahlen sind 1, 3, 6, 10,15 und 21
Ich hoffe der Artikel hat euch gefallen.