Vielleicht seid ihr schon über den Begriff Dreieckszahlen gestolpert, vielleicht seid ihr auf diesem Gebiet ja auch Experten! Aber vielleicht fragt ihr euch was das bloss sein mag.
Definition:
Eine Dreieckszahl ist die Summe von der Zahlen 1 , .... , n. Sprich: 1+2+...+n.
Das lässt sich auch schön über das Summenzeichen schreiben: \( \sum_{i=1}^{n} ~ i ~~\). Das ist das griechische Sigma: ∑.
Ihr fragt euch was das Ganze mit Dreiecken zu tun hat? Schaut her:
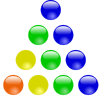
Rot = 1, Gelb = 2, Grün = 3, Blau = 4 und die Summe ist eine Dreickszahl.
Die erste Dreieckszahl ist 1. Bei manchen Autoren ist auch 0 eine Dreieckzahl, darüber lässt sich streiten, das ist genau wie die 0 und IN.
Berechnung:
1. Dreickszahl: 1
2. Dreickszahl: 3
3. Dreickszahl: 6
4. Dreickszahl: 10
...
n. Dreieckzahl: \( ~\frac{n \cdot (n+1)}{2}~\)
Es ist viel zu viel Arbeit die 100. Dreieckzahl Summand für Summand zu berechnen, klar. Dieser Meinung war auch der "kleine" Gauss:
In seiner Grundschulzeit bekamen er und seine Klassenkameraden von ihrem faulen Lehrer die Aufgabe alle Zahlen von 1 bis 100 zu addieren. Der Lehrer freute sich auf eine freie Stunde, ohne viel zu Arbeiten. Doch nicht mit Gauss! Er rechnete nicht wie die anderen Kinder einfach drauf los, nein, er war schlauer:
Er rechnete: (50+51) + (49+52) + (48+53) + ... + (1+100) = ...
Jede dieser Klammern ergibt 101, jede Zahl von 1 bis 100 ist benutzt. Es gibt 50 solcher Klammern:
... = 50*101 = 5050.
Binnen weniger Minuten musste sich der Mathelehrer eine neue Aufgabe für Gauss überlegen.
Aus diesem System lässt sich die Formel \(\sum_{i=1}^n \;i\;\; = \; \frac{n\cdot (n+1)}{2}\) überlegen. Beweisen lässt sie sich über vollständige Induktion. Kleine Übungsaufgabe für dich, Emre ;)
Bei Interesse, hier genaueres: http://www.mathematische-basteleien.de/dreieckszahlen.htm