Geometrie: Quadrat mit. Symmetrieachsen

Question

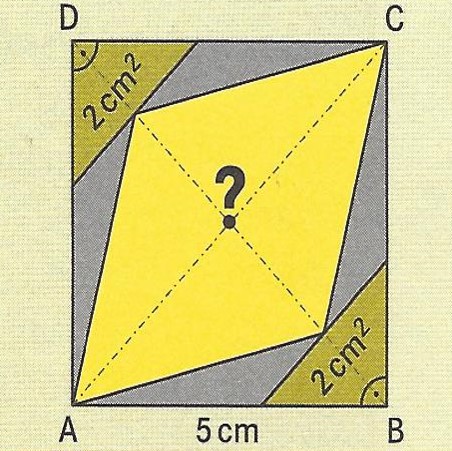
ABCD ist ein Quadrat mit einer Seitenlänge von 5 cm. Die Gesamtfigur hat 2 Symmetrieachsen.

Mein Lösungsansatz:

Ich finde den Einstieg nicht richtig. Nehme an, dass das rechtwinklige/gleischschenklige Dreieck (je 2 cm")der Schlüssel ist?

Die vier 3-ecke (von Mitte in die Ecken sind ja je 6.25 cm2. Das Quadrat daraus also 12.5 cm2, die Strecke z.B. D bis Mitte 3.5355 minus die 1 cm von D bis Schnittstelle gelber Drache und Dreieck (2 cm2). Ergäbe also 2.5355 x 2 = 5.071 cm für die gelbe Diagonale D-B (minus die Dreiecke 2 cm2)?????

Besten Dank für Eure Mithilfe.

Comments

Gesucht ist vermutlich die Fläche mit dem Fragezeichen drin, oder?

Überlege mal, was es mit den grünen Dreiecken auf sich hat!

Wie könnte man deren Kantenlängen oder gar die Höhe bestimmen?

---

Vom "Der Mathe_Coach" hat die Lösung mit Hilfe des Pythagoras-Satzes gelöst.  Wir hatten diesen aber noch nicht in der Schule. Kann man diese Frage nicht auch lösen, ohne Pythagoras anwenden zu müssen?

Besten Dank.

Answer 1

Ich habe dazu ein kurzes knappes Video gemacht. Ich bitte die schlechte Qualität zu entschuldigen.

Comments

Wir lernen den Satz des Pythagoras erst im nächsten Kapitel. Diese Frage sollte also auch ohne Pythagoras möglich sein, oder?

Besten Dank.

---

Ja sicher. Du kannst ein graues Dreieck ausrechnen

Agrau = 1/2 * g * h = 1/2 * (5 - 2) * (2/2) = 1.5 cm²

Damit ergibt sich jetzt die gelbe Fläche

Agelb = 5 * 5 - 2 * 2 - 4 * 1.5 = 15 cm²

---

Jetzt ist alles klaro, besten Dank!!!

Answer 2

https://www.geogebra.org/m/wcu4Tvuc

zeigt die Möglichkeit ohne Pythagoras zur Fläche zu kommen, indem die Dreiecke anders angeordnet betrachtet werden.

Viel Spaß !