Supremum, Infimum bestimmen in einer komplexen Zahlenfolge

Question

!

ich sitze schon mega lange vor der folgenden Aufgabe, komme aber einfach nicht drauf. Vielleicht könnt ihr ja helfen?

Sei (z_n) n ∈ ℕ komplexe Zahlenfolge mit:

$$ { z }^{ n }:={ i }^{ n }+\frac { 1 }{ 2 } \bullet { (\frac { 1+i }{ \sqrt { 2 }  } ) }^{ n } $$

Bestimmen Sie:

(a) sup({Re(z_n) : n ∈ ℕ}).

(b) inf({Im(z_n) : n ∈ ℕ}).

(c) sup({|z_n| : n ∈ ℕ}). 

Answer 1

Zuerst einmal solltest du dir das Verhalten der Folge für große \(n\) ansehen. \(\left(\frac{1+i}{\sqrt2}\right)^2=\frac12 +\frac{2i}{2}+\frac{i^2}2=i.\)

Also hat der erste Summand Periode 4: \(i^4=(-1)^2=1=i^0,\) während der zweite Term Periode 8 hat: \(\sqrt i^8=1=\sqrt i^0.\)

Also ist \(z_n=z_{n-8}=...=z_k\) für \(k\equiv n \mod 8,\) also insbesondere \(1\leq k \leq 8.\)

Damit musst du nur acht Folgenglieder untersuchen.

$$i+\frac12\left(\frac{1+i}{\sqrt2}\right)\\-1+\frac12i\\-i+\frac12i\left(\frac{1+i}{\sqrt2}\right)\\1+\frac12(-1)\\i+\frac12(-1)\left(\frac{1+i}{\sqrt2}\right)\\-1+\frac12(-i)\\-i+\frac12(-i)\left(\frac{1+i}{\sqrt2}\right)\\1+\frac12$$

Da sowohl \(i\) als auch \(\sqrt i\) Länge eins haben, sind Multiplikationen mit diesen Zahlen nur Rotationen, also ist \(1+\frac12\) garantiert der größtmögliche Realteil (die Summe zweier Vektoren fester Länge ist maximal, wenn sie beide parallel sind und die Projektion auf die \(x\)-Achse ist maximal, wenn die Vektoren parallel zur \(x\)-Achse sind). Gleichzeitig ist dies auch das Supremum des Betrages, weil auch der Betrag zweier Vektoren maximal ist, wenn sie parallel sind. Also \(\sup\{\Re(z_n)|n\in \mathbb N\}=\sup\{|z_n|\ |n\in \mathbb N\}=\frac 32.\)

Das Infimum des Imaginärteils ist etwas schwieriger, weil man wirklich alle durchgehen muss, weil die Rotation nie so zusammenfällt, dass die Imaginärteile beider Summanden parallel nach unten zeigen. Es stellt sich heraus, dass der vorletzte Eintrag minimalen Imaginärteil hat:

$$-i+\frac12(-i)\left(\frac{1+i}{\sqrt2}\right)=-i\left(1+\frac{1+i}{2\sqrt2}\right)=\frac1{2\sqrt2}+i\left(-\frac{2\sqrt2+1}{2\sqrt2}\right).$$

Also \(\inf\{\Im(z_n)|n\in \mathbb N\}=-\frac{2\sqrt2+1}{2\sqrt2}.\)

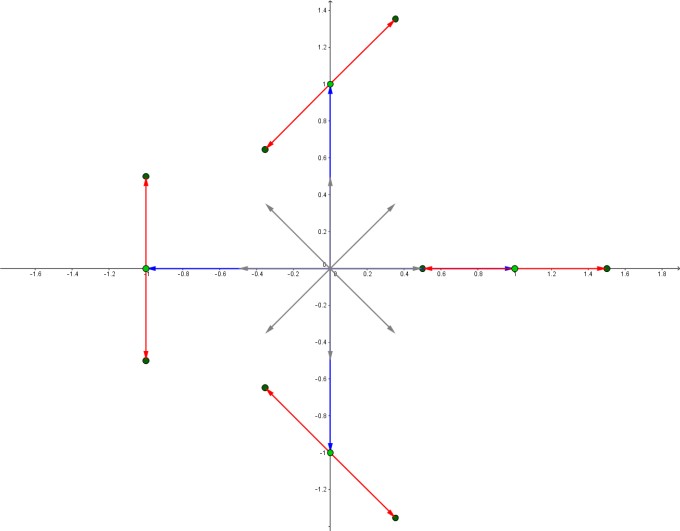Blaue Vektoren: \(i^n\), graue Vektoren \(\frac12 \sqrt i^n\), rote Vektoren: graue Vektoren an den entsprechenden blauen Vektoren abgetragen, dunkelgrüne Punkte: \((z_n)_{n\in \mathbb N}.\)

Comments

Danke schon mal für deine tolle Antwort. Sitzen jetzt zu 8. an der Aufgabe und wissen nicht, warum du die 2 für n am Anfang einsetzt. Wir probieren einfach alle 8 Perioden für den 2. Term durch, geht das auch?

---

Hey :) ich hab auch nochmal eine Frage zu deiner Lösung

---

und zwar, warum der zweite Summand √i ist

---

Der zweite Summand ist \(\sqrt i\), weil er mit sich selbst multipliziert \(i\) ergibt. So wie \(3^2=9 \Rightarrow 3=\sqrt9.\) Dabei ist das \(\sqrt i\) mehr eine Notationssache, weil es zwei komplexe Zahlen gibt, deren Quadrat \(i\) ergibt. So wie \(\sqrt9=-3\) genausogut wie \(3\) sein könnte. Bei den reellen Zahlen gibt es die Konvention, die positive der beiden Zahlen zu nehmen, im Komplexen nicht. Aber zumindest ist sicher, dass das Quadrat der Zahl die Zahl \(i\) ergibt, und das ist hier das einzig Wichtige.

Natürlich kann man auch solange probieren, bis man auf eine Periode stößt, das Quadrieren bot sich hier eben an, um zu zeigen, wie die beiden Summanden sich unabhängig voneinander entwickeln, und bei Summen ist die Periode einfach das kleinste gemeinsame Vielfache der Perioden der Summanden.

Eine Art Trick, um schneller aufs selbe Ergebnis zu kommen.