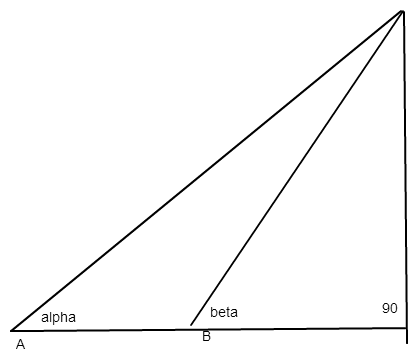
Die drei Orte A, B und C liegen in einer Ebene. Wie hoch ist der Berggipfel über der Ebene?

Question

Die drei Orte A, B und C liegen in einer Ebene . Die Entfernung AB beträgt 3250m. Von einem Berggipfel G aus sieht man A und B in derselben Richtung, unter dem Tiefenwinkel alpha= 10,8

und Beta = 18,6 

Nach Drehen des Messinstrumentes um den Horizontalwinkel ε = 38,5 misst man zu C den Tiefenwinkel φ 12,1

 

a.)Wie hoch ist der Berggipfel über der Ebene ? ( das hab ich noch geschafft)

b.) Wie weit ist C von A bzw. B entfernt ?

c.)Wie groß ist der Flächeninhalt des Dreiecks, das von den drei Orten A, B, C gebildet wird??

 

Comments

Anmerkung: Die Frage wurde von Anonym erneut gestellt, im Folgenden die Kommentare daraus:

Mathecoach hat diese Aufgabe schon vorgerechnet.

Möglicherweise musst du noch einen Rechenfehler finden. Weiss nicht, ob du derselbe Anonym bist.

---

ja bin ich das Ergebnis stimmt aber nicht überein ...

---

und du findest bei Mathecoach keinen Fehler? Oder verstehst du irgendetwas an der Antwort nicht? Sag bitte, was.

Resultate in Unterlagen stimmen nicht immer. In Mathebüchern werden sie etwa ab der vierten Auflage zuverlässig.

---

bei mir ist das Ergebnis 6.75 km^{2 ..}

jetzt bin ich mir nicht sicher ob bei der Lösung ein Fehler vorliegt, oder von Mathecoach

---

Dann vergleich doch deine Lösung mit meiner. Ich habe meine nicht auf Fehler geprüft. Das überlasse ich immer dem Fragesteller. Du solltest meine Rechnung Schritt für Schritt durchgehen und verstehen und dort wo du etwas anderes hast durch nachrechnen dann den Fehler melden.

Ich mache extra vorher keine Fehlerkontrolle damit sich der Fragesteller intensiv mit dem Ansatz beschäftigt. Ich möchte hier keine abschreibefertige Lösungen posten. Sonstern die Musterlösung sollte von dir selber kommen.

Answer 1

a.)Wie hoch ist der Berggipfel über der Ebene ? ( das hab ich noch geschafft)

h = 1431 m

nur zur Kontrolle. Die anderen Ergebnisse kommen.

Comments

AC = √((1431/TAN(10.8°))^2 + (1431/TAN(12.1°))^2 - 2·(1431/TAN(10.8°))·(1431/TAN(12.1°))·COS(38.5°))

AC = 4739 m

BC = √((1431/TAN(18.6°))^2 + (1431/TAN(12.1°))^2 - 2·(1431/TAN(18.6°))·(1431/TAN(12.1°))·COS(38.5°))

BC = 4267 m

---

Gamma = arccos((a^2 + b^2 - c^2) / (2 * a * b))
Gamma = arccos((4739^2 + 4267^2 - 3250^2)/(2·4739·4267))
Gamma = 41.90 Grad

A = 1/2 * a * b * cos(Gamma)
A = 1/2 * 4739 * 4267 * cos(41.90)
A = 7525478 m^2 = 753 ha

---

hallo mathecoah

es sollte 6753613,7 hinaukommen für die quadratmetern
das steht in meiner Lösung
LG

---

ich denke der Winkel 41.90 ist falsch

gehört nicht 38,5 ??

---

Du meinst das dreieck am Boden hat den gleichen Winkel um den ich das Instrument drehen muss. Warum meinst du das?