a) Die Gleichungen für E und E habe ich raus.b) Man setzt E und E gleich. Wie löse ich aber das Gleichungssystem? Ich habe drei Gleichungen mit vier Variablen?
Was sind die Ansätze zu c) und d)?
Aufgabe:
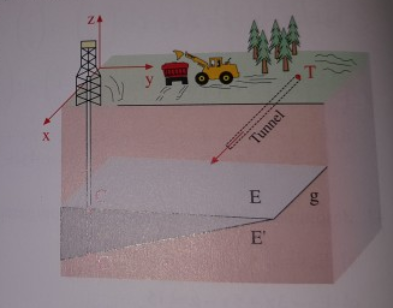
Ein keilförmiges Kohleflöz hat nach oben und unten ebene Begrenzungsflächen E und E' zu den angrenzenden Gesteinsschichten. Bei drei Probebohrungen werden jeweils der Eintrittspunkt und der Austrittspunkt festgestellt:
A (-20|30|-200), A' (-20|30|-236), B (120|180|-80), B' (120|180|-120), C (80|120|-120), C' (80|120|-160).
a) Wie lauten die Gleichungen der Begrenzungsebenen E und E'?
b) Wie lautet die Gleichung der Geraden g, in der das Kohleflöz endet?
c) vom Punkt T (-200|200|0) wird ein Tunnel in Richtung des Vektors \( \begin{pmatrix} 2\\-2\\-1 \end{pmatrix} \) vorangetrieben. Wo trifft er die Kohleschicht, wo verlässt er sie wieder, wie weit ist es vom Tunneleingang bis zur Kohleschicht?
d) Trifft eine senkrechte Bohrung, die im Punkt T (-100|450|0) beginnt, die Kohleschicht?
\( \left(\begin{array}{c}{-20} \\ {30} \\ {-200}\end{array}\right)+u\left(\begin{array}{c}{140} \\ {150} \\ {120}\end{array}\right)+v\left(\begin{array}{c}{100} \\ {90} \\ {80}\end{array}\right)=\left(\begin{array}{c}{-20} \\ {30} \\ {-236}\end{array}\right)+s\left(\begin{array}{c}{140} \\ {150} \\ {116}\end{array}\right)+t\left(\begin{array}{c}{100} \\ {90} \\ {76}\end{array}\right) \)