hier sind einige Konstruktionsvorschläge aufgetaucht, die für Schüler der Klasse 7 nicht nachvollziehbar sind. Die Aufgabe ist im Asbach Uralt-LS (G9 BW), in der letzten Ausgabe (G8 BW) nicht, jetzt aber wieder in der aktuellen (G8 BW, Bildungsplan 2016) enthalten. Meine Tochter hatte sie heute als Hausaufgabe auf und aus diesem Grund hier die Lösung mit den Mitteln eines Siebtklässlers für alle Interessierten mit Geogebra dargestellt:
Konstruktionsanleitung:
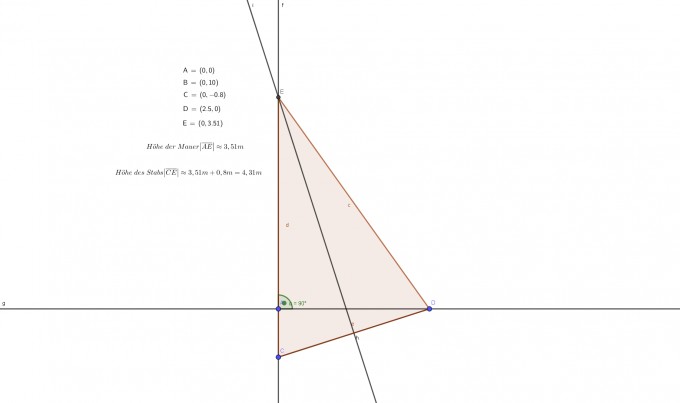
• Zeichne eine (waagrechte) Gerade \(g\).
• Zeichne eine dazu orthogonale Gerade \(h\). Der Schnittpunkt sei \(A\).
• \(C∈h\) liegt 0,8 LE unterhalb \(A\).
• \(D∈g\) liegt 2,5 LE rechts von \(A\).
• Konstruiere die Mittelsenkrechte auf der Strecke \( \overline {CD} \)
• Der Schnittpunkt der Mittelsenkrechte mit \( h \) sei \( E \)
• Höhe des Stabs \( \left| \overline{CE} \right| \approx 4,31m \)
• Höhe der Mauer \( \left| \overline{AE} \right| \approx 4,31m-0,8m=3,51 m \)
Warum ist das so?
Die Bedingungen sind, dass der Stab 0,8m länger als die Mauer bzw. die Mauer 0,8m niedriger als der Stab ist und das Ende des Stabs 2,5 m vom Fußpunkt der Mauer entfernt steht, wenn der Stab bündig mit der Oberkante der Mauer abschließt.
Die Mittelsenkrechte ist die Ortslinie, die alle Punkte markiert, die von zwei Punkten gleich weit entfernt sind (in diesem Fall \(C\) und \( D \). Der Schnittpunkt der Gerade \(h\) mit der Mittelsenkrechte (Punkt \( E \) ) bildet mit den Punkten C und D ein gleichschenkliges Dreieck, dessen Schenkel die Länge des Stabs bilden. Trägt man am linken Schenkel 0,8 LE ab erhält man aus dem Rest des Schenkels die Höhe der Mauer. Da man \( D \) zuvor im Abstand 2,5 LE von \( A \) gewählt hatte, sind beide Bedingungen efüllt.
Ich hoffe, ich konnte damit alle Klarheiten beseitigen.
Es grüßt euch der Mathepauker