Geometrie - Kreiskonstruktionen 8. Klasse

Question

Hi,

gegeben ist das quadrat abcd. Konstruiere alle kreise, welche durch C verlaufen und die Seitan ab und ad berühren.

Meine Frage:

Wie macht man die Skizze und den dazugehörigen Konstruktionsbericht.

Answer 1

Hi,

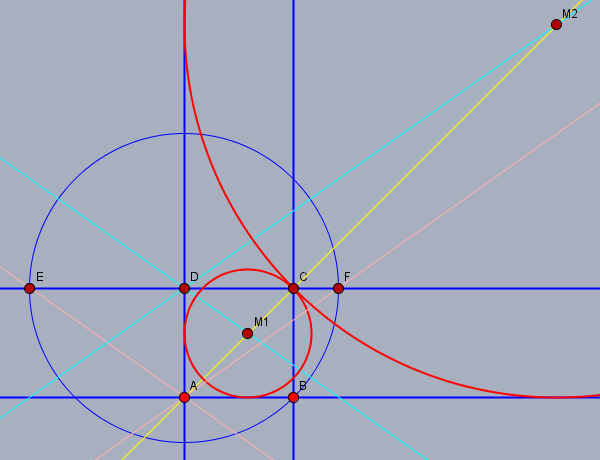
zeichne das Quadrat ABCD, inklusive der Diagonalen AC (gelb). Dann schlage einen Kreis k (blau) um D mit dem Radius DB, der die Verlängerung von CD in E und F schneidet. Zeichne die beiden Geraden durch AE und AF (rosa). Dann konstruiere die beiden Parallelen zu den Geraden durch AE und AF, die durch den Punkt D laufen (hellblau). Die Parallelen schneiden die Gerade durch AC (gelb) in den Punkten M₁ und M₂.

Die Kreise um M₁ und M₂ durch C sind die gesuchten Kreise.

zur Erklärung: M₁ teilt die Strecke CA im Verhältnis 1:\(\sqrt{2}\). Das Verhältnis von CD:DB bzw. CD:DE ist ebenfalls 1:\(\sqrt{2}\). Nach Strahlensatz ist CD:DE=CM₁:M₁A.

C teilt die Strecke M₂A im Verhältnis 1:\((\sqrt{2}-1)\). Genauso teilt C die Strecke DF im selben Verhältnis. Lt. Strahlensatz (Zentrum ist C) sind die Geraden durch DM₂ und AF parallel.

Gruß Werner

Comments

Danke vielmals!

Ich habs jetzt tip top kapiert