Trigonometrie: In einem rechtwinkligen Dreieck sind nur die Winkel gegeben.

Question

Aufgabe a.)

In einem rechtwinkligen Dreieck ABC ist  sin alpha = 0,6 und cos alpha = 0,8

( sin alpha = 0,5 und tan Alpha = 1/3*Wurzel aus 3).

Berechne tan alpha  (cos alpha).

Aufgabe b.)

Gib für die Seiten a,b,c des Dreiecks eine Verhältniskette a:b:c mit natürlichen Zahlen an.

Comments

In einem rechtwinkligen Dreieck ABC ist  sin alpha = 0,6 und cos alpha = 0,8

( sin alpha = 0,5 und tan Alpha = 1/3*Wurzel aus 3).

Gib für die Seiten a,b,c des Dreiecks eine Verhältniskette a:b:c mit natürlichen Zahlen an.

---

Hallo

siehe www.mathelounge.de/408065/

Grüße,

M.B.

---

Aufgabe B ist hier wichtig.

---

Die kannst du ausrechnen, wenn du a) hast.

Answer 1

Aufgabe b)

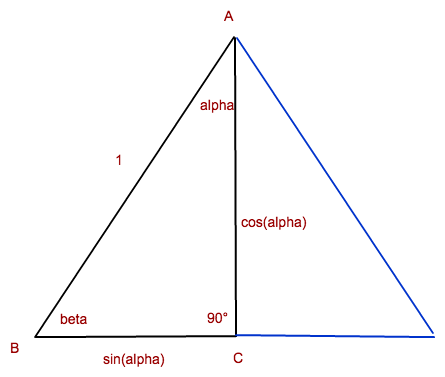
Nur linker Teil der Skizze ist relevant. Nimm einfach mal die Hypotenuse als 1 an.

Dann hast du a : b : c = sin(alpha) : cos(alpha) : 1       | sin alpha = 0,6 und cos alpha = 0,8

a : b : c = 0.6 : 0.8 : 1         | alle Zahlen mal 5 rechnen (5 ist Hauptnenner)

a : b : c = 3 : 4 : 5 

Analog mit der Klammeraufgabe. (???)

Dann hast du a : b : c = sin(alpha) : cos(alpha) : 1       | ( sin alpha = 0,5 und tan Alpha = 1/3*√3 = √3 / 3 )

tan(alpha) = sin(alpha)/cos(alpha)

cos(alpha) = sin(alpha)/tan(alpha)= 1/2 (3/√3) = 1/2 (√3) = √3/2 . 

a : b : c = 1/2  : (√3/2) : 1         | alle Zahlen mal 2 rechnen (2 ist Hauptnenner)

a : b : c = 1 : √3 : 2 

Hier bekomme ich allerdings kein ganzzahliges Ergebnis hin. Findest du einen Fehler? 

Comments

ja  Vorgabe (√3 / 3 ) und eingesetzt wurde (√3 / 2)

aber eine ganze Zahl finde ich trotzdem nicht

---

Das war gemäss Fragestellung der tangens(alpha). Ich musste ja erst noch den cosinus(alpha) ausrechnen.

Answer 2

Du kennst (hoffentlich) \( \tan = {\sin \over \cos} \). Damit kannst Du alles berechnen.

Grüße,

M.B.