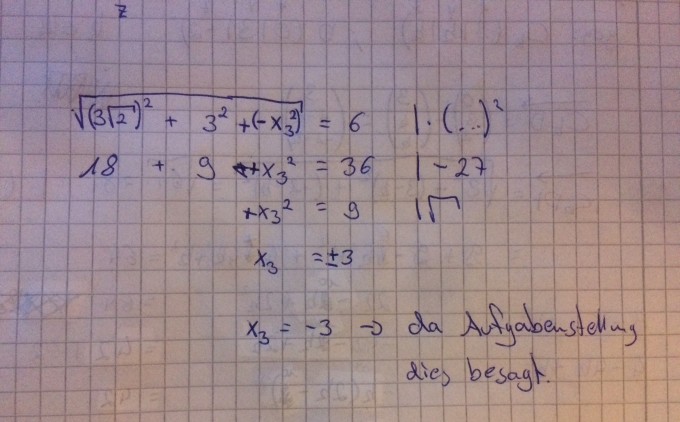Bestimmen Sie alle Komponenten des Vektors x mit a) x bildet mit x-Achse Winkel von 45° ,...

Question

Leider komme ich nicht weiter als hier:

$$ |\vec{ x }|=\sqrt { { x }_{ 1 }²+{ x }_{ 2 }²+{ x }_{ 3 }² } =6 $$

Ich hoffe einer kann mir ein wenig unter die Arme greifen. Vielen dank!

Comments

Wenn es um Winkel zwischen Vektoren geht, kannst du das Skalarprodukt benutzen.

https://de.wikipedia.org/wiki/Skalarprodukt

---

Spielt es keine Rollte, ob es Vektoren oder eben die X/ Y-Achse ist?

---

Für die x- und y-Achse brauchst du einen (möglichst einfachen) Richtungsvektor.

Bsp. (1,0,0) und (0,1,0)

Answer 1

x* ( 1;0;0) = 6 * 1 * cos(45°)

x1 = 6 * 1 * cos(45°) = 3√2

analog:

x*(0;1;0) = 6 * 1 * cos(60°)


x2 = 3

und

x1² + x2² + x3² = 36

2*9  + 9 + x3² = 36

x3= - 3  wegen   x3 <  0

Comments

super Vielen dank für deine Antwort :)
Mir stellen sich jetzt nur zwei Fragen:

x1 = 6 * 1 * cos(45°) = 3√2 

6 ist ja die Gesamtlänge

cos 45° ist ja der Winkel zur X-Achse

aber woher nimmst du die 1?

Gleiches bei der 2. Rechnung.

__

Und was du in der letzten Zeile gemacht hast, da blicke ich noch nicht ganz hinter... Ich habe es so gelöst:

---

Die letzte Zeile bestand bestimmt aus mehreren Zeilen. Da hat der Editor mathef einen Streich gespielt.

---

Habe es korrigiert. Hatte irgendwie < und > verwechselt !

und zu    :

x1 = 6 * 1 * cos(45°) = 3√2 

6 ist ja die Gesamtlänge

cos 45° ist ja der Winkel zur X-Achse

aber woher nimmst du die 1?     Das ist die Länge von ( 1 ;0;0) .

---

Ja aber woher nimmst du die Länge?

Nimmst du das einfach so an? Weil das ist ja nirgends gegeben
Das versteh ich nicht so ganz..

---

Es gilt ja allgemein :Skalarprodukt von a und b

=  Länge von a * Länge von b * cos des Winkels