Cosinus (x + ( pi / 2)) Wieso?? Ableitung

Question

ich hätte da mal eine Frage bezüglich der 1. Ableitung von cos(x+(π/2))

Als ersten Punkt hätte ich den Grafen der Cosinusfunktion um π/2 verschoben.

 

Somit käme bei mir der Graf der Sinusfunktion heraus.

die Ableitung von sin(x) wäre cos(x) aber als Lösung kommt -cos(x) heraus.

könntet ihr mir bitte sagen, was ich falsch mache.

MRRRR

Answer 1

COS(x + π/2)

Typischer Fehler. Das "+ π/2" verschiebt den Graphen der Cosinusfunktion um "π/2" nach LINKS und nicht nach rechts.

Comments

wieso nach links und nicht nach rechts

---

Du kennst eventuell die Scheitelpunktform der Parabel.

y = (x + 2)^2

Wie ist da die Parabel verschoben. 2 nach rechts oder links?

Warum 2 nach links?

Weil du etwas an der Stelle (x + 2) berechnest und dieses dann eben bei x abträgst also 2 Einheiten weiter links.

---

also muss man bei allen Funktionen den Wert nach dem x immer nach links verschieben, da dieser Wert von der x skala nach links gezogen wird

---

Steht dort "x + 2" verschiebt sich das um 2 nach links,

steht dort "x - 2" verschiebt es sich um 2 nach rechts.

---

danke dir für die gute Antwort

---

Hier einmal weil ich es gerade habe zeichnen
lassen

Answer 2

Eine Verschiebung in Richtung y-Achse erfolgt wie
gedacht

y = x
y = x + 4 ( nach oben )
y = x - 4 ( nach unten )

Jetzt schau dir einmal deinen Graph an.

y = cos ( x ) für x = 0
y = cos ( 0 ) = 1

y = cos ( x + π / 2 ) für x = 0
y = cos ( 0 + π / 2  )  = 0
Nicht wie bei dir + 1

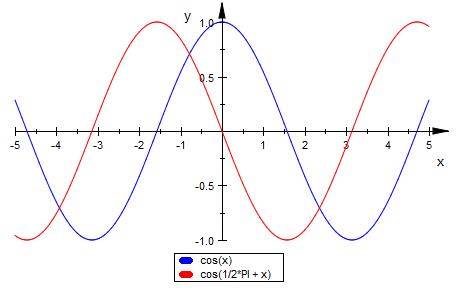
Hier die beiden Funktionen im Vergleich
Die Ausgangsfunktion wird nach links verschoben.
und entspricht der -sin ( x ) Funktion.