Aufgabe 5. Rotationskörper. Wie hoch steht die Flüssigkeit, wenn Behälter nicht rotiert?

Question

Es geht um folgende Aufgabe. Stimmen meine Lösungen für a)-c)  und wie löse ich d)?

Wasser rotiert
Ein Behälter mit Wasser rotiert. Die Wasseroberfläche nimmt unter dem Einfluss der Fliehkraft und der Schwerkraft ein parabelförmiges Profil an.
a) Bestimmen Sie die Gleichung der quadratischen Funktion \( f(x)=a x^{2}, \) die das Profil der Wasseroberfläche darstellt.
b) Berechnen Sie die Umkehrfunktion von f.
c) Berechnen Sie das Flüssigkeitsvolumen.
d) Wie hoch steht die Flüssigkeit, wern der Behälter nicht rotiert, sondern in Ruhe ist?

Meine Lösungen:

a) \( f(x)=\frac{3}{4} x^{2} \)
b) \( f^{-1}(x)=\sqrt{\frac{4}{3} x} \)
c) \( V=37,7 \text{ VE} \)
\( d) \,? \)

Answer 1

Unglücklichsterweise ist meine 1.Antwort
verschwunden. Hier einmal die Kurzform

r = √ ( 4 / 3 * x )
A = r^2 * π = 4 / 3 * π
V =  ∫ A dx zwischen 0 und 3
V ( Rotation ) = 6 * π

h = 4
V ( Zylinder ) = 2^2 * π * h = 16 * π

( 16 - 6 ) * π = 10 * π

d.)
10 * π = 2^2 * π * h
h = 2.5

Comments

Ich habe c) so gerechnet:

---

Warum steht da eine 2 vor dem pi vor dem Integral. Die gehört da nicht hin. Sonst richtig.

---

Man soll doch das Volumen von der blauen Fläche bestimmen oder?

Es gibt doch zwei blaue Flächen, die durch die y-Achse getrennt werden...

---

Ja genau. Man geht so vor. Man berechnet erst einen großen Zylinder den es gar nicht gibt. Da kommt 16pi raus. Von diesem zieht man das volumen ab, dass sich innerhalb der Parabel befindet. Dieses bekommt man durch Integration zu 6pi. Dadurch erhält man das restliche (blaue) volumen zu 10pi.

---

Wie kommt man denn auf einen Zylinder?

---

Naja, dir ist schon klar dass das ein runder Topf ist, der sich da dreht, oder? Also ist das volumen in dem Topf ein Zylinder mit der Höhe 4.

---

16π ist also das Volumen des Zylinders und 10π das Volumen der blauen Fläche.

Was ist dann 6π für eine Fläche? Von 0 bis 3 oder?

Aber dann verstehe ich nicht wieso man dann die Differenz bildet?

---

Und wie kommt man auf diesen Ansatz:

10 * π = 2² * π * h

?

---

Also wir haben ja ermittelt dass das gesuchte volumen 10pi ist. Wenn sich der Topf nicht dreht gibs keine parabel sondern das Wasser steht einfach in dem Topf in der Form eines zylinders. Das volumen des zylinders ist pi*r^2*h wobei r=2 ist also 4*pi*h.

---

          

---

Eine Frage noch:

Wo sind die 6pi in der Zeichnung?

---

Ich habe die 6pi mal orange schraffiert.

---

Kann man sagen: Man bestimmt das Volumen der blauen Fläche? Oder ist das mathematisch nicht korrekt?

---

Streng genommen hat eine Fläche kein volumen. Sag doch lieber du bestimmst das volumen der Flüssigkeit, die in der Abbildung blau dargestellt ist.

---

kleine Fehlerkorrektur in meiner Antwort

anstelle
r = √ ( 4 / 3 * x )
A = r² * π = 4 / 3 * π
muß es heißen
A = r² * π = 4 / 3 * x * π

Ansonsten stimmt alles.

---

Ich habe noch zwei Fragen...

c) Man bestimmt ja das Volumen innerhalb der Parabel und erhält 18,85 VE. Muss man das nicht  mal 2 nehmen, da wir zwei Seiten im Grunde haben? Also wieso hat man für die Integrationsgrenzen nicht folgendes bestimmt: f(-2) und f(2)?

Und entsteht immer ein Zylinder, wenn man eine Parabel um die y-Achse oder x-Achse rotiert?

---

Ich will mir nicht noch einmal alles
durchlesen. Deshalb nochmals die
Herleitung.
Zusehen ist eine Parabel
Beim Rotieren um die y-Achse bildet die
Parabel die Innenfläche des Wassers

Für eine einfachere Berechnung wird das Bild
um 90 ° nach rechts gekippt.
Jetzt rotiert alles um die x-Achse.
Die Formel der ehemaligen Parabel lautet nun
f ( x ) = √ ( 4 / 3 * x )
Zeichne an beliebiger Stelle x  den Funktionswert
f (x ) als Strich ein.
Dieser Strich rotieret um die x-Achse und
bildet einen Kreis. f ( x ) ist der Radius des
Kreises.
f ( x ) = r = √ ( 4 / 3 * x )
Die Fläche des Kreises ist
A = r² * π = 4 / 3 * x * π

Nun werden alle Kreisflächen zwischen 0 und
3 aufsummiert. Dies ist der Hohlraum. ( orange )

∫ A ( x ) dx zwischen 0 und 3

Das Wasser befindet sich zwischen -1 bis 3
und bildet einen Zylinder.
r = 2
A = r^2 * pi = 2^2 * Pi
∫ A dx  zwischen -1 und 3
Einfacher gehts natürlich über die Zylinderformel
r^2 * pi * h ( h = 4 )

Zum Schluß heißt es
Zylindervolumen minus Hohlraum = Volumen Wasser

Bitte beachten : die durch Rotation entstehenden
Kreisflächen werden aufsummiert,
nicht die blaue Fläche im Bild.

---

Vielleicht könntest Du konkret auf meine Fragen eingehen...

---

hallo probe,

Ich habe noch zwei Fragen...

c) Man bestimmt ja das Volumen innerhalb der Parabel und erhält 18,85 VE.
Muss man das nicht  mal 2 nehmen, da wir zwei Seiten im Grunde haben? Also wieso hat man für die Integrationsgrenzen nicht folgendes bestimmt: f(-2) und f(2)?

Ich meine den Fehlergund für alles bei dir zu kennen.
Den habe ich zu Anfang auch gemacht.

Du siehst in der Abbildung eine blaue Fläche und meinst
diesen Flächenihalt bestimmen zu müssen
bzw.
den Flächeninhalt innerhalb der Parabel.

∫ f ( x ) dx zwischen 0 und +2 für die rechte Seite
und
∫ f ( x ) dx zwischen -2 und 0 für die linke Seite

zusammen

∫ f ( x ) dx zwischen -2 und +2 für beides

Damit hast du nur die angezeigte 2-dimensionale
SCHNITTFLÄCHE berechnet.

Die Parabel rotiert aber um eine Achse im RAUM.

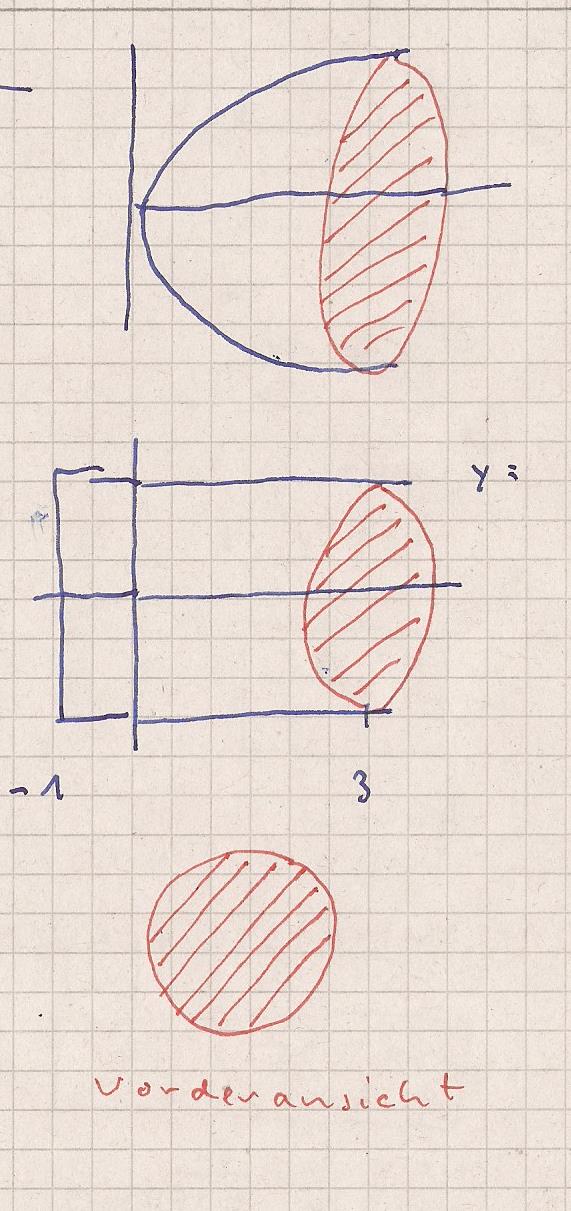
Es entseht ein Körper den ich zur Volumenberechnung in Scheiben
schneide und diese aufsummiere. Ich summiere Kreise auf wie
dir die Vorderansicht  zeigt.

Und entsteht immer ein Zylinder, wenn man eine Parabel
um die y-Achse oder x-Achse roti

Nein. Bild 2 zeigt dir eine Gerade im Abstand 2 von der
x-Achse. Wenn diese Gerade um die x-Achse rotiert entsteht
ein Zylinder.

---

Leider ist das mir immer noch nicht ganz klar. Das liegt wohl an mir. Trotzdem bedanke ich mich für die Hilfe.

---

beim Teil d hast du falsch gedacht

2,5 ist die maximale Höhe des Zylinders. man sollte 6π gleich Volumen des Zylinders setzen.

---

Das ist ja ein irre langer thread.
Ich möchte mich aber nicht mehr
damit beschäftigen.
Eine von den Antworten die hier
eingestellt wurden wird wohl
eine richtige Antwort sein.

Answer 2

Die Lösungen zu a) un b) habe ich auch. Bei c) habe ich 10π als Volumen. Der Radius des Behälters ist 2, also muss ich h bestimmen im Ansatz π·4h=10·π also h=5/2.

Comments

Wie kommt man auf diesen Ansatz?:

π·4h=10·π

---

Wie kommt man auf diesen Ansatz?: π·4h=10·π

Das Volumen eines Zylinders mit dem Radius 2 und der Höhe h ist π·2²·h und das soll gleich dem Volumen des Rotationskörpers sein (ich hab da 10π heraus).

Answer 3

Hallo probe,

Das Volumen V des Wasser erhältst du, wenn du die Fläche A1 und die Fläche A2 um die y-Achse rotieren lässt und die Ergebnisse  V1 und V2 addierst.

Bei A1 rotiert ein Rechteck, das ergibt dann ein Zylindervolumen

              V₁ = r² * π * h =  2² * π * 1

Für V2 lässt du das Rechteck A2+A3 rotieren und ziehst dann das Rotationsvolumen von A3 ab:

V2 = 2² * π * 3 -  π * ₀∫³ (√(4/3 x))² dx

V = V1 + V2

d) 

Wenn der Behälter (das ist ein Zylinder)  nicht rotiert, bildet das ruhende Wasser im Behälter selbst einen Zylinder mit dem gleichen Volumen  V  und einer gesuchten Höhe h:

V = 2² * π * h     →   h  = V / (4π)  [Längeneinheiten]

da h bei y = -1 anfängt, steht das Wasser nur bis y = h - 1

Sollten noch Fragen sein: ich bin da :-)

Gruß Wolfgang

Comments

Mir ist das jetzt klar.

Eine Frage habe ich noch:

Wieso rechnet man nicht jeweils V1 und V2 mal 2, weil wir das doch auch auf der linken Seite haben...

---

Wenn z.B. das Recheck  A1 um die y-Achse rotiert, werden die Raumpunkte auf der linken Seite mit erfasst. Dadurch entsteht als Rotationsvolumen direkt ein Zylinder.

---

Und wie sieht es damit aus:

π * ₀∫³ (√(4/3 x))² dx 

Wieso setzt man vor dem pi keine 2?

vielleicht wegen der Umkehrfunktion?

---

Ja, mit der Umkehrfunktion  x = f^-1(y)  gilt bei Rotation um die y-Achse - analog zur Rotation um die x-Achse - immer

V_y  =  π * _y1∫^y2 [ f ^-1(y) ]² dy      (die Integrationsvariable y kann man dann auch x nennen, weil sie ja sowieso durch die Grenzen ersetzt wird)

---

Ich meine wieso berechnet man nicht:

2π * ₀∫³ (√(4/3 x))² dx 

Auf der linken Seite gibt es doch auch diese Fläche oder nicht?

---

Das ist der gleiche Grund wie vorher:

Wenn die Fläche A2 auf der rechten Seite um die y-Achse rotiert, werden die Raumpunkte auf der linken Seite mit erfasst.

---

               

---

Freut mich, wenn du es verstanden hast :-)

---

Warum hat man einen Zylinder, wenn der Behälter nicht rotiert? Wenn er nicht rotiert, dann hat man doch gar kein Körper oder?

Was hat man dann, wenn der Behälter rotiert?

---

Wenn der Behälter nicht rotiert, ist doch das Wasser immer noch da.

Es bedindet sich unten im Behälter in Ruhe und hat die Zylinderform des Behälters.

Das Volumen dieses "Wasserzylinders" ist das gleiche wie das Wasservolumen während der Rotation. Nur hat der "Wasserkörper" dann die Form einer Vase.

---

Was ich nicht ganz verstehe, wieso entsteht dann eine Vaser, wenn man das rotiert.

Der Behälter bleibt doch einfach vorhanden?

---

Hallo probe,
irgendwie scheint dir das Rotieren von
Funktionen um Koordinatenachsen
mächtig Schwierigkeiten zu bereiten.

Schau dir bitte die Lernvidoes an

---

@probe

nicht der Behälter, sondern das Wasser, das beim Rotieren des Behälters durch die Zentrifugalkraft zum Teil an den Wänden des Behälters hochsteigt, hat dann die Form einer Vase (oder Obstschale)

Hier geht es immer nur um das Volumen des Wassers.

---

Hallo Wolfgang,

Beim Lesen deiner Antwort kommt mir folgende Frage in den Sinn :
Kann denn aber die Form des Behälters die Form des rotierenden Wassers beeinflussen?

Liebe Grüße Tanya

---

                   

---

@Tanya

Natürlich zwingt die Form des Behälters dem Wasser außen seine Form auf. Die Form der Oberfläche ist aber in der Aufgabe vorgegeben.

---

Hallo Wolfgang

Ich meinte nicht die Form außen, sondern innen.

Wenn sich in dem schwarzen zylinderförmigen Behälter die blaue Wasseroberfläche einstellt,

 

welche Oberfläche ergibt sich dann z.B. in dem roten kegelförmigen Behälter?

Liebe Grüße Tanya