f(x)=0,017*x^2, warum ist an jeder Stelle des Rotationskörpers der Inhalt pi*f(x)^2

Question

ich verstehe das nicht so. Wir haben die Parabel 0.017*x^2 und lassen sie um ihre Symmetrieachse rotieren, sodass wir einen Parabloiden bekommen. Warum stimmt die Aussage: Der Inhalt der Querschnittsfläche des Rotationskörpers ist an jeder Stelle x pi*f(x)^2. Ich verstehe nicht, warum das so ist...

Answer 1

die Symmetrieachse ist die y-Achse. Die Querschnitsfläche des Rotationskörpers an einer Stelle x ist ein Kreis mit dem Radius |x|.

→  A = π • x² 

A = π • f(x)²  wäre bei Rotation um die x-Achse richtig. 

Gruß Wolfgang

Answer 2

Hier die Zusammenhänge

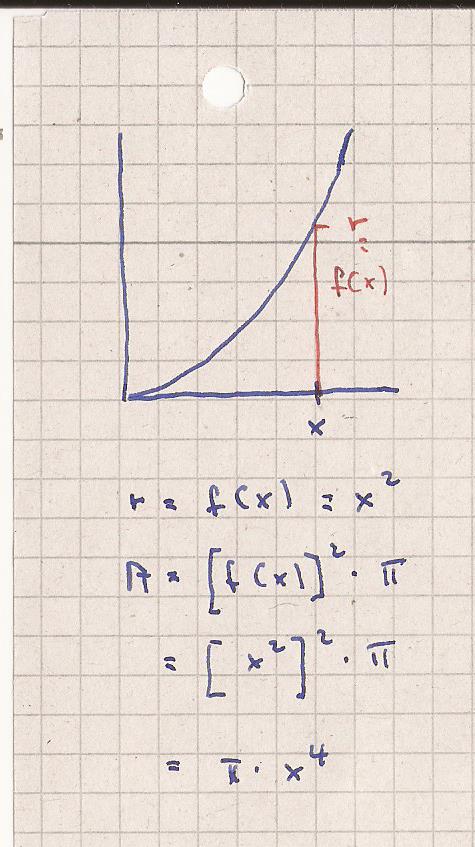
r ist der Radius des Kreises bei Rotation um
die x-Achse.  r entspricht f ( x ) an der Stelle x.

A = Fläche = r^2 * π
A = ( f ( x ) )^2 * π

lassen sie um ihre Symmetrieachse rotieren,
Die Symmetrieachse für f wäre die y-Achse.
Wäre auch möglich.