Strecke zwischen 2 Umkreise berechnen?

Question

Ich bin auf der Suche nach Rat, ich versuche verzweifelt folgende Fragen zu lösen und zwar,

1) wie lang ist, wenn man bei der unten angeführten Skizze die Umkreise beider rechtwinkligen Dreiecke einzeichnet, die kürzeste Strecke zwischen diesen innerhalb des gleichschenkligen Trapez ABA'B'?

2) wie groß ist nach einzeichnen der Umkreise die Verbelibende Fläche des Trapez ABA'B'?

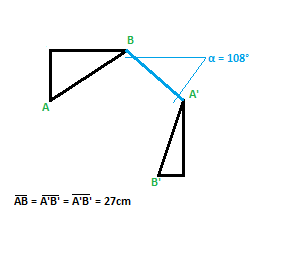
ich bin für jede Hilfe bereits im voraus sehr dankbar. 

Answer 1

Bedenke, dass der Umkreis eines rechtwinkligen Dreiecks gleichzeitig der Thaleskreis über der Hypotenuse ist. Folgendes Bild zeigt das:

 

Somit ist der Radius \(r_U\) der Umkreise in beiden Fällen \(r_U=AB/2\). Der grüne Winkel ist \(108°-90°=18°\) und mittels Sinus kann man die Strecke \(UE\) berechnen.Weiter gilt, dass \(UU'=BA'+2\cdot UE\) und der Abstand der Umkreise \(GH=UU'-2\cdot r_U\) ist.

Die verbleibende Fläche Trapez minus Kreisausschnitte schaffst Du jetzt alleine. Betrachte das Dreieck \(AFU\) und den Kreissektor \(BUF\). Ziehe beides zweimal von der Fläche \(F_T=UU' \cdot BF\) des Trapez ab.

Falls noch Fragen offen sind, bitte melden.

Answer 2

1) Die Mittelpunkte der Umkreise der gegebenen (rechtwinkligen) Dreiecke lieben in der Mitte ihrer Hypotenusen. Ihr Abstand ist gleich der Länge der Mittelparallelen des gleichschenkligen Trapezes. Mit a=AB' und c=A'B ist das (a+c)/2.

2) wie groß ist nach Abzug der Umkreise die verbleibende Fläche des Trapez ABA'B'?

Die Trapezfläche habe die Höhe h und den Inhalt h·(a+c)/2. Von ihr ist ein Vollkreis mit dem Durchmesser b=B'A' zu subtrahieren, also π·(b/2)².

Comments

Hallo Roland,

Du schreibst: "Die Trapezfläche habe die Höhe h und den Inhalt h·(a+c)/2. Von ihr ist ein Vollkreis mit dem Durchmesser b=B'A' zu subtrahieren, also π·(b/2)². "

Das ist ein wenig zu viel abgezogen. Beachte das Kreissegment zwischen den Punkten A und F in meiner Antwort.

---

Du hast natürlich recht. Ich hatte mir keine Skizze angelegt und genau berachtet.