Stochastik Glücksrad: Welchen Gesamtgewinn darf die Klasse erwarten, wenn 100 Spiele zustande kommen?

Question

Aufgabe Stochastik:

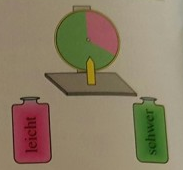
Für ein Fest organisiert die Klasse 12a ein Ratespiel, um die Klassenkasse aufzubessern. Der Spieler dreht das Glücksrad mit einem roten und einem doppelt so großen grünen Sektor einmal. Zeigt der Zeiger auf das rote Feld, erhält der Spieler eine Frage aus der roten Urne, welche leichte Fragen enthält. Zeigt der Zeiger auf das grüne Feld, erhält der Spieler eine Frage aus der grünen Urne mit schweren Fragen.

Die Klasse schätzt, dass ein normaler Spieler durchschnitlich 50 % der leichten und 25 % der schweren Fragen richtig beantworten kann.

a) Alexander führt testweise ein Spiel durch. Wie groß ist die Wahrscheinlichkeit, dass er die Frage richtig beantwortet?

b) Alexander spielt sechsmal. Wie groß ist die Wahrscheinlichkeit, dass er mehr Fragen richtig als falsch beantwortet?

c) Für ein Spiel wird 1 € als Einsatz verlangt. Wird die Frage richtig beantwortet, bekommt der Spieler 2 € ausgezahlt. Welchen Gesamtgewinn darf die Klasse erwarten, wenn 100 Spiele zustande kommen?

d) Mit welchen Wahrscheinlichkeit sind nach 100 Spielen mindestens 40 € in der Klassenkasse? Hinweis: Überlegen Sie zunächst, wie viele der 100 Spiele die Spieler hierfür höchstens gewinnen dürfen.

c) Durch Verkleinerung des roten Sektors auf dem Glücksrad soll erreicht werden, dass bei 100 Spielen im Durchschnitt 40 € für die Klassenkasse bleiben. Wie groß müssen die Sektoren auf dem Glücksrad gewählt werden?

Probleme:

Ich habe Probleme mit den Aufgaben b) und c)

Mein Ansatz bei b) ist:

1/3 x 0,25^2 + 1/3 x 0,25 = 10,41 %

Ich dachte mir, dass man 4 mal richtige Antworten braucht und dann 2 Falsche oder 5 mal richtige und 1 mal eine Falsche Antwort.

Also Lösung die vorgegeben wurde steht jedoch : 1-0,899 = 10,01 %

bei c)

hier dachte ich mir als Ansatz:

0,50 x 50 = 25€

0,25 x 50 = 12,50€

unterm Strich würde das ein Gewinn von 12,50€ ergeben bei 100 mal Spielen.

in der Musterlösung steht als Ergebnis jedoch -2x1/3 + 1 = 1/3

Answer 1

K sei das Ereignis, dass die Frage  richtig beantwortet wird. Die Wahrscheinlichkeit für K hast du in Teil a) ausgerechnet.

b)

> 4 mal richtige Antworten braucht und dann 2 Falsche oder 5 mal richtige und 1 mal eine Falsche Antwort.

Die dritte Möglichhkeit fehlt in dieser Aufzählung.

X sei die Anzahl er richtigen Anworten. X ist binomialverteilt mit p=P(K) und n = 6

Berechne P(X=4) + P(X=5) + P(X=6).

c)

E = 100·(-1·P(K) + 1·(1-P(K)))

Answer 2

a)

P = 1/3 * 0.5 + 2/3 * 0.25 = 1/3 = 33.33%

b)

P = ∑(COMB(6, x)·(1/3)^x·(2/3)^{6 - x}, x, 4, 6) = 73/729 = 10.01%

c)

100·(1 - 1/3·2) = 33.33 €

d)

100·1 - x·2 ≥ 40 --> x ≤ 30

P = ∑(COMB(100, x)·(1/3)^x·(2/3)^{100 - x}, x, 0, 30) = 0.2766 = 27.66%

e)

100·1 - x·2 = 40 --> x = 30

a·0.5 + (1 - a)·0.25 = 0.3 --> a = 1/5

1/5 des Rades sollte für leichte Fragen stehen und 4/5 für schwere Fragen.

Comments

Wie gebe ich es richtig im Taschenrechner ein bei deiner Lösung in Aufgabe b?

---

Also du musst die (mit hilfe der binomialverteilung) angegebe Wahrscheinlichkeit ausrechnen indem du für x die Werte 4, 5 und 6 einsetzt. Du bekommst 3 Werte raus die du zusammenrechnen musst.

---

Das hängt vom verwendeten Taschenrechner ab. Bei der Casio- Reihe könnte ich helfen. Mit anderen Rechnern kenne ich mich nicht so gut aus.