1. Aufgabe
Die roten Kreisscheiben haben der Radius r = a/8 . Ihre Fläche ist F = π*r^2 = π(a/8)^2 = π(a^2)/64
Es sind 16 rote Kreise. Gesamtfläche der Kreise 16 * (π(a^2)/64) = π(a^2)/4
Gesamtfläche des Quadrates ist a^2
Nun die Prozentzahl ausrechnen.
Anteil ist (π(a^2)/4 ) / a^2 = π/4 ≈ 0.785398 also ca. 78.5398 Prozent.
Bemerkung: π(a^2)/4 = π*(a/2)^2 . Das ist die Fläche eines Kreises, der mit Radius a/2 genau in das grosse Quadrat passt. Du hättest direkt diese Kreisfläche nehmen können um die gefragte Prozentzahl auszurechnen.
Grund: In jedem Teilquadrat ist der Anteil der roten Fläche an der Gesamtfläche gleich gross:
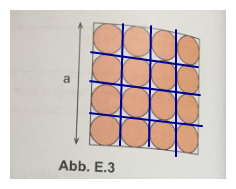
Skizze von 2. (mache sie etwas grösser, damit du genug Platz hast)
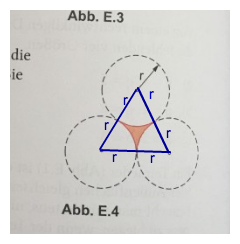
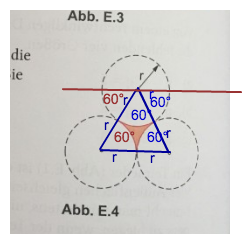
Die weisse Fläche im gleichseitigen Dreieck ist die Fläche eines Halbkreises mit Radius r.
F_(weiss) = (r^2 * π) / 2
Jetzt brauchst du noch die Fläche des gleichseitigen Dreiecks.
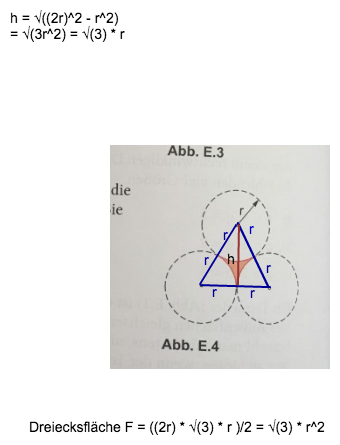
F_(rot) = √(3) * r^2 - (r^2 * π) / 2 = (√(3) - π/2) * r^2