Geben sie mit Hilfe der Variablen a einen Term für die Fläche des Dreiecks ABM an

Question

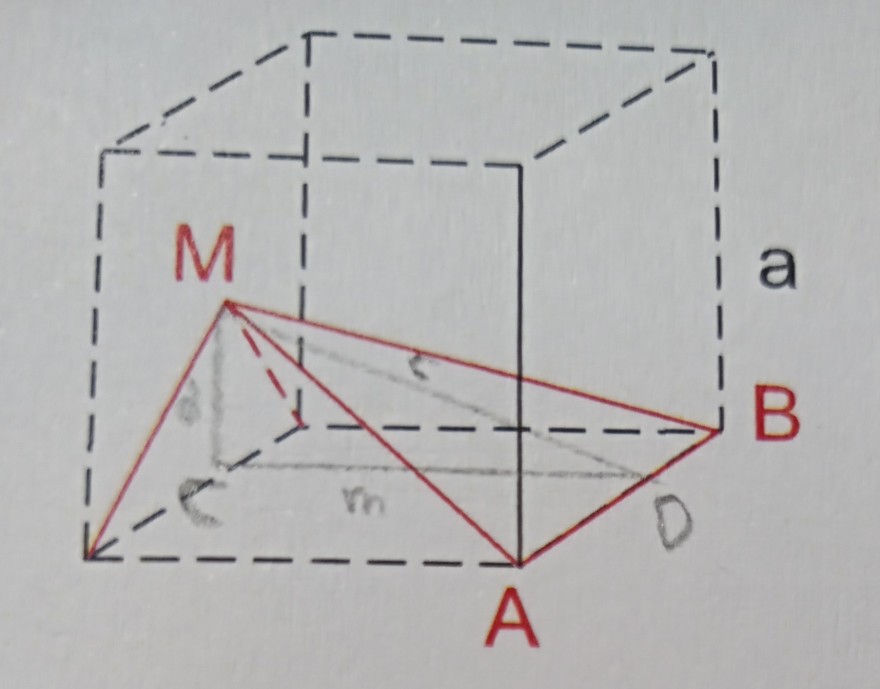
Aufgabe: Geben sie mit Hilfe der Variablen a einen Term für die Fläche des Dreiecks ABM an.

Hallo an alle!

Diese Aufgabe wurde hier bereits vor einiger Zeit beantwortet, leider stoße ich trotzdem auf ein Problem, welches ich nicht verstehe.

Um das eingezeichnete Dreieck AMB zu berechnen, fehlt die Höhe h. Diese lässt sich durch das (von mir eingezeichnete) Dreieck CDM berechnen und stellt dort die Hypotenuse c dar.

Nun habe ich folgendes Problem:

Versuche ich durch den Satz des Pythagoras die fehlende Seite c (und damit die Höhe im gesuchten Dreieck) zu berechnen, so komme ich zu keinem Ergebnis.

a^2 + b^2 = c^2 | umgestellt und an Variablen angepasst

c^2 = m^2 - d^2  | eingefügt

c^2 = a^2  - (1/2a)^2

Berechne ich nun, so löst sich a^2 - (1/2a)^2 miteinander auf, wenn ich das richtig sehe. Ich lande also bei c^2=0.

Aber wieso? Wo ist hier mein Denkfehler? Ich würde es gerne verstehen, aber aktuell führt jeder von mir gewählte Weg in eine Sackgasse.


Ich bedanke mich schon einmal für jede Antwort!

Comments

Warum löst sich das zu Null auf?

$$a^2 - \frac{1}{4} a^2 = \frac{3}{4} a^2$$

---

c^{2} = m^{2} - d^{2}  | eingefügt

$$c^{2} = m^2 {\color{red}+} d^2 = a^2 + \left(\frac{a}{2}\right)^2 = \frac{5}{4} a^2$$

---

Vielen Dank, ich glaube darin lag mein Fehler!

Answer 1

\( \overline{MD} \) = \( \begin{pmatrix} -a\\0\\\frac{a}{2} \end{pmatrix} \). Der Betrag davon ist die Höhe im Dreieck ABM.

Answer 2

\(c^2 = a^2  - (\frac{1}{2}a)^2=a^2- \frac{1}{4}a^2=\frac{3}{4}a^2\)

\(c =\frac{a}{2}\sqrt{3}\)