Du kannst das Ganze auch unmittelbar mittels Vektoren beweisen, ohne den
Satz über die Seitenhalbierenden im Dreieck zu bemühen.
Etwa so:
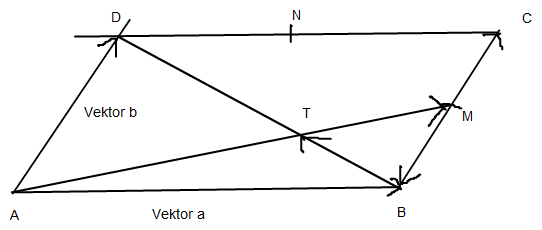
Vektorkette BT + TM + MB = 0-Vektor
also mit geeigneten Faktoren x und y gilt dann
mit den Basisvektoren a und b
x*BD + y*AM - 0,5*b = 0 - Vektor
x* ( -a +b ) + y * ( a + 0,5 b ) - 0,5 b = 0 - Vektor
sortiert nach a und b
( -x+y)*a + ( x+0,5y - 0,5 ) * b = 0 - Vektor
Da a,b lin. unabh. sind: -x+y=0 und x+0,5y - 0,5 = 0
also x = y = 1/3
Also BT = (!/3) BD . q.e.d.
Für den Teilpunkt N entsprechend (wenn AN die Diagonale
bei S schneidet ) mit dem Ansatz
SD + DN + NS = 0-Vektor