Hallo Aynika,
Zeichen ein Zeit-Weg-Diagramm und zeichne alles ein, was in der Aufgabe gegeben ist:
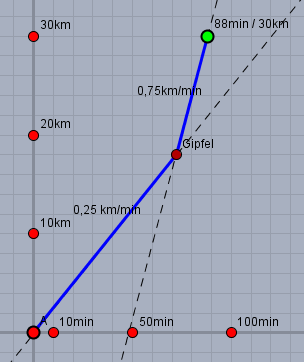
Der Startpunkt ist der Koordinatenursprung. Nach rechts läuft die Zeit und nach oben die Geschwindigkeit. Nach 1h:28min hat Sonja die 30km zurück gelegt. Das ist der grüne Punkt oben rechts. Sie hatte auf der Bergfahrt eine Geschwindigkeit von$$v_B = 15 \frac{\text{km}}{\text{h}} = 0,25 \frac{\text{km}}{\text{min}}$$ Das ist die Gerade, die vom Ursprung startet und eine Steigung von \(0,25\) hat. Auf der Talfahrt war ihre Geschwindigkeit $$v_B = 45 \frac{\text{km}}{\text{h}} = 0,75 \frac{\text{km}}{\text{min}}$$Das ist die Gerade, die durch den Zielpunkt verläuft und eine Steigung von \(0,75\) hat.
Jetzt braucht man bloß noch den Schnittpunkt der beiden Geraden zu berechnen und dann weißt Du, zu welcher Zeit (der x-Wert) und nach wie vielen Kilometern (der y-Wert) Sonja auf dem Gipfel war.
Die beiden linearen Funktionen sind: $$\begin{aligned} s_B(t) &= 0,25 \frac{\text{km}}{\text{min}} t \\ s_T(t) &= 0,75 \frac{\text{km}}{\text{min}} (t-88 \text{min}) + 30 \text{km}\end{aligned}$$Kommst Du alleine damit klar? Lösung: \(t_G= 72\text{min}\) bei \(18 \text{km}\). Sonst frage bitte nach.
Gruß Werner