Funktionsgleichung und Steigung gegeben. Berührungspunkt gesucht.

Question

Ich habe bei der folgenden Aufgabe ein Problem und weiss nicht, wie ich diese Lösen kann.

Geg: Normalparabel mit der Funktionsgleichung: p(x) = x^2

Jetzt soll eine Tangente an die Normalparabel gelegt werden, dass die Steigung dieser 41 ist.

Ges: Berührungspunkt, den man jetzt bestimmen muss.

Am besten wäre eine Lösung in Zwischenschritten, die leicht verständlich ist,

 

Answer 1

"Steigung" bedeutet "erste Ableitung". f '(x)=2x. Dann soll gelten: 2x=41 und x=20,5. Die Tangente geht durch den Punkt (20,5; 420,25).

Answer 2

Hallo

ich stelle dir die Antwort hier im Forum ein.
Zunächst eine Skizze

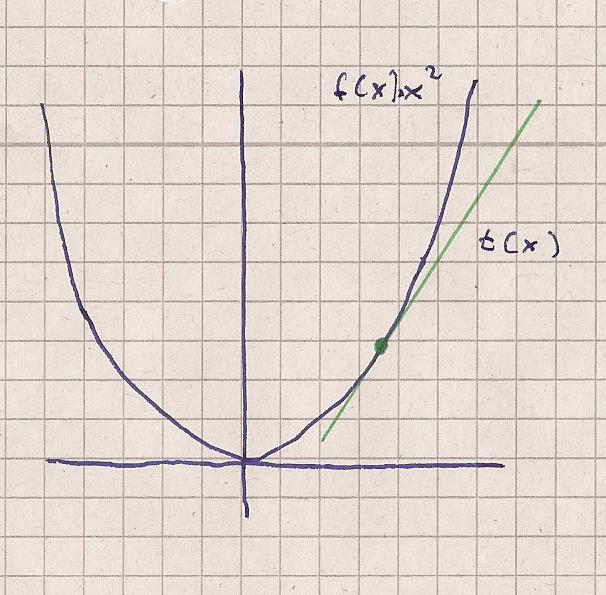
Für einen Berührpunkt gilt
f ( x ) = t ( x )  | gleiche Koordinaten
f ´( x ) = t ´( x )  | gleiche Steigung.

Ich denke dies ist in der Skizze gut sichtbar.

f ( x ) = x^2
f ´( x ) = 2 * x
t ( x ) = m * x + b
t ´( x ) = m

Die Steigung der Parabel im Berührpunkt ist mit 41
angegeben
f ´( x ) = 2 * x = 42
x = 20.5
Der Funktionswert der Parabel an der Stelle x = 20.5 ist
f ( 20.5 ) = 20.5^2 =  = 420.25

B ( 20.5 | 420.25 )

Damit ist die gestellte Frage bereits beantwortet.

Mitunter wird auch nach der Funktionsgleichung der
Tangente gefragt.
f ´( 20.5 ) = t ´( 20.5 ) = m
m = 41

t ( x ) = 41 * x + b
b ist noch unbekannt. Nun den Berührpunkt einsetzen.
t ( 20.5 ) = 41 * 20.5 + b = 420.25
41 * 20.5 + b = 420.25
b = - 420.25
t ( x ) = 41 * x - 420.25

Ja mehr Aufgaben du rechnest desto mehr wirst
du dich auch verbessern. Garantiert.

Bei Bedarf wieder nachfragen.

mfg Georg

Comments

Ich habe noch den Graph vergessen