zunächst mal eine Skizze
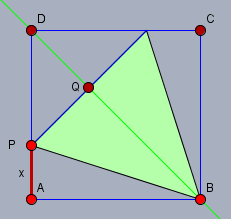
Das Dreieck PQD ist ein gleichschenkliges und rechtwinkliges Dreieck, d.h. dass die Strecke \(PQ=DQ=\frac{1}{2}\sqrt{2} PD\) lang ist. Mit dieser Information lässt sich die Fläche des grünen Dreiecks in Abhängigkeit von \(x\) bestimmen. Es gilt
$$F(x)=PQ \cdot QB= \frac{1}{2}\sqrt{2} PD \cdot (BD - DQ) \\= \frac{1}{2}\sqrt{2} (a-x) \cdot (a\sqrt{2} - \frac{1}{2}\sqrt{2} (a-x)) \\= a(a-x) - \frac{1}{2}(a-x)^2$$
nach \(x\) ableiten und Ableitung zu 0 setzen ergibt
$$F\prime (x)=-a+(a-x_{opt})=0 \quad \Rightarrow x_{opt}=0$$
Gruß Werner