Eine Frage bezüglich meiner Lösungsansätze ;
Es geht um die Funktion
\( N\left(" p 1^{\prime \prime}, " p 2^{\prime \prime}\right)=\frac{1}{\ln \left(" p 1^{\prime \prime *} p 2^{\prime \prime}\right)} \)
a) Gesucht ; "Ökonomisch" sinnvoller Definitionsbereich D ... sowie das Skizzieren von D.
Meine Antwort:
\( D=\left\{\left({" p} 1^{\prime \prime, "} p 2^{\prime \prime}\right) \in R^{2}++\mid " p 2^{\prime \prime} \neq\left(\frac{1}{{ }^{\prime \prime} p 1^{\prime \prime}}\right) \quad\right\} \)
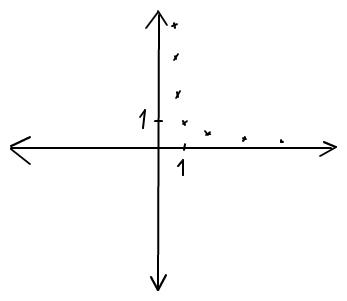
b) Die Frage , ob ein Steigen von p1 eine steigende oder fallende Nachfrage bewirkt ...
Meine Antwort :
\( \frac{\delta N}{\delta^{\prime \prime} p 1^{\prime \prime}}=\frac{-1}{" p 1^{\prime \prime *}\left(\ln \left({ }^{\prime \prime} p 1^{\prime \prime *^{\prime \prime}} p^{\prime \prime \prime}\right)\right)^{2}}<0 \)
Nachfrage fällt .
Bei a und b bin ich mir eigentlich ziemlich sicher, dass sie zutreffen .
Bei Frage c weiß ich nicht, was ich tun soll.
c) Skizzieren Sie die Bereiche von D , in denen die Nachfrage elastisch , unelastisch bzw. einselastisch auf Veränderungen von "p1" reagiert. (Hinweis: Achten Sie darauf, dass der Betrag von "E" untersucht wird.)