Neutrales Element eines booleschen Ausdruck finden

Question

Sei M eine endliche Menge mit n-Elementen und P(M) die Potenzmenge von M, Auf P(M) kann man eine Operation ° wie folgt beschreiben.

X,Y Element  P(M), X°Y = (X Y) \ (X Y)

Exististiert in (P(M), °) ein neutrales Element?

Exististiert in (P(M), °) ein inverses Element?

Welche algebraische Struktur besitzt (P(M), °)?

^∩

Answer 1

Hallo jf,

X o Y = ( X ∪ Y ) \  ( X  ∩ Y  )

∅  ist  neutrales Element, denn

X o ∅  =  ( X ∪ ∅ ) \ ( X  ∩ ∅ )  =  X \ ∅  =  X    für alle x ∈ P(M) 

X  ist inverses Element  zu X, denn

 X o X    =  ( X ∪ X ) \  ( X  ∩ X )  = X \ X  =  ∅   für alle x ∈ P(M) 

----------

Wegen der Kommutativität von ∪ und ∩ gilt offensichtlich das Kommutativgesetz.

Assoziativgesetz:  (XoY) o Z = X o (YoZ)  ? 

[ [ ( X ∪ Y ) \  ( X  ∩ Y  ) ] ∪ Z ] ]   \   [ [ ( X ∪ Y ) \  ( X  ∩ Y  ) ] ∩  Z ] ]    

               =  [ X ∪ [ ( Y ∪ Z ) \  ( Y ∩ Z  ) ] ]   \  [ X ∩ [ ( Y ∪ Z ) \  ( Y ∩ Z  ) ] ]       ?

Die beiden Seiten der Gleichung  ergeben  im Venn-Diagramm jeweils 

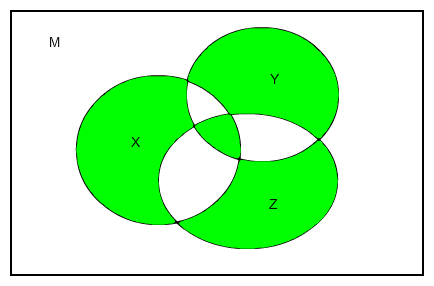
Damit ist (M,o) eine abelsche Gruppe  

Info:

https://de.wikipedia.org/wiki/Abelsche_Gruppe

Gruß Wolfgang

Comments

 X¯¯¯¯ = M \ X  wäre inverses Element zu X, wenn ...

 

---

Hatte es inzwischen korrigiert.