Ich finde die Aufgabe etwas schwieriger, als die, auf die Der_Mathecoach verweist. Zumal die Aufgabe IMHO nicht eindeutig ist. Es heißt "... und nach der Bewegung mit reduzierter Winkelgeschwindigkeit über eine Zeit von 300 ms gleichförmig beschleunigt." Auf was bezieht sich hier das 'eine Zeit von 300ms'. Heißt das, dass die reduzierte Geschwindigkeit 300ms gehalten wird und dann wird beschleunigt oder dass eine Zeitlang mit reduzierter Geschwindigkeit gefahren wird und dann 300ms lang beschleunigt wird. Ich unterstelle mal letzteres.
Ich würde auch das Erstellen des \(\omega,t\)-Schaubildes vorziehen, das erleichtert die Sache ziemlich.
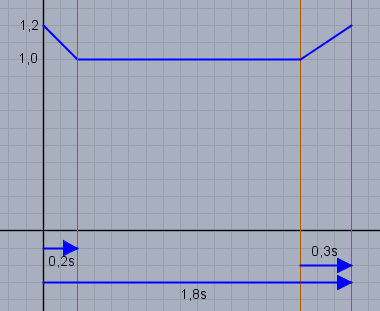
Die Winkelgeschwindigkeit im ersten Bereich folgt einer linearen Funktion über der Zeit:
$$\omega(t)=\omega_0 + \dot{\omega}\cdot t=1,2\frac{1}{\text{s}} - 1 \frac{1}{\text{s}^2}\cdot t$$
Daraus ergibt sich die Winkelgeschwindigkeit nach 0,2s zu \(\omega(0,2\text{s})=1,0\frac{1}{\text{s}}\). Um zum Winkel nach 0,2s zu kommen, reicht es jetzt die Kästchen zu zählen. Da der Winkel das Integral über die Geschwindigkeit ist. In obiger Skizze entspechen 100Kästchen dem Wert 1 - ich zähle 22 - also muss \(\varphi(0,2\text{s})=0,22\) sein. Die Rechnung sähe so aus:
$$\int_0^{0,2\text{s}}1,2\frac{1}{\text{s}} - 1 \frac{1}{\text{s}^2}\cdot t \space dt = 1,2 \cdot 0,2 - \frac{1}{2}0,2^2=0,24-0,02=0,22\approx 12,6° $$
Um den Gesamtwinkel zu bestimmen, könnte man wieder Kästchen zählen - ich komme diesmal auf 185 -also einen Winkel von 1,85rad. Ausrechnen lässt sich das natürlich auch:
$$\varphi(1,5s)=0,22 + \int_{0,2\text{s}}^{1,5\text{s}}1 \frac{1}{\text{s}} \space dt=0,22 + 1 \frac{1}{\text{s}}(1,5\text{s}-0,2\text{s})=0,22+1,3=1,52$$
Für das letzte Stück fehlt noch die Beschleunigung. Die ist \(\dot{\omega}=\frac{\Delta \omega}{\Delta t}=\frac{0,2{\text{s}}^{-1}}{0,3\text{s}}=\frac{2}{3}\text{s}^{-2}\) also ist:
$$\varphi(1,8s)=1,52 + \int_{1,5\text{s}}^{1,8\text{s}}1 \frac{1}{\text{s}} + \frac{2}{3}\frac{1}{\text{s}^2}\cdot (t-1,5\text{s}) \space dt$$
$$\space = 1,52 + 1 \frac{1}{\text{s}}(1,8\text{s}-1,5\text{s}) + \frac{1}{3}\frac{1}{\text{s}^2}(1,8\text{s}-1,5\text{s})^2=1,52 + 0,3+0,03=1,85 \approx 106,0°$$
Gruß Werner