Hochpunkt, Tiefpunkt und Sattelpunkt bestimmen: f(x) = x^3 - 2x und f(x) = x^3 - 2x - 5 und f(x) = 3x^3

Question

Kann mir bitte jemand weiterhelfen, wie ich bei diesen drei Aufgaben weiter rechnen muss? (bitte mit Rechnung)

a) f(x) = x^3 - 2x

f'(x) = 3x^2 -2

0 = 3x^2 -2

2/3 = x^2

-> ich bekomme hier doch +/- Ergebnisse, was soll ich dann machen?

b) f(x) = x^3 - 2x - 5

f'(x) = 3x^2 -2

0 = 3x^2 -2

2/3 = x^2

c) f(x) = 3x^3

f'(x) = 9x^2

Answer 1

a) f(x) = x³ - 2x

f'(x) = 3x² -2

0 = 3x² -2

2/3 = x²

-> ich bekomme hier doch +/- Ergebnisse, was soll ich dann machen?

Richtig. Rechne beide Resultate aus. Der Graph hat somit an beiden Stellen die Steigung 0. Nun kannst du mit beiden weiterrechnen.

b)  f(x) = x³ - 2x - 5

f'(x) = 3x² -2

0 = 3x² -2

2/3 = x²

Hier auch.

c) f(x) = 3x³

f'(x) = 9x²

Hier bekommst du x1 = x2 = 0. Doppelte Nullstelle der ersten Ableitung.

Comments

Bei a) sind die x-Werte ja x1= √2/3 und x2= -√2/3. Ich habe diese x-Stellen dann in die Funktion f(x) = x³ - 2x eingesetzt und als Lösung -4√6/9 erhalten. Nach der Lösung ist aber y-Wert 4/3 √2/3. Was mache ich den falsch?

---

Die Wurzel aus einem Bruch kann man auch anders darstellen:

https://www.wolframalpha.com/input/?i=sqrt(2%2F3)&lk=1&rawformassumption=%22ClashPrefs%22+-%3E+%7B%22Math%22%7D 

Setze bitte Klammern um die Radikanden, damit zu sehen ist, wie weit die Wurzeln gehen. Hast du ein Bild deiner Rechnung?

---

Hoffe das hilft weiter.

---

(√(2/3) )^3

= √((2/3)^3)

= √((2/3)^2 * (2/3)^1)       | teilweise Wurzelziehen

= 2/3 * √(2/3)

Nun davon noch 2*√(2/3) subtrahieren

f(√(2/3)) = (2/3 - 2) * √(2/3)

= (2/3 - 6/3)*√(2/3)           | Bruchsubtraktion

= -4/3 * √(2/3)

Answer 2

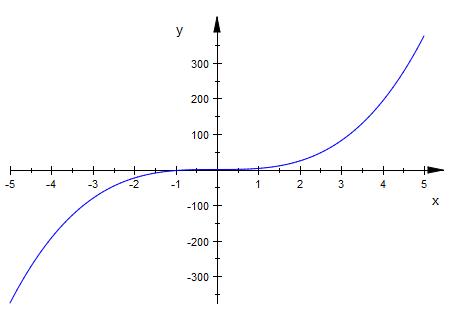
c)

f ( x ) = 3 * x^3
f ´( x ) = 9 * x^2
f ´´ ( x ) = 18 * x

Stelle mit waagerechter Tangente
1.Ableitung = 0

f ´( x ) = 9 * x^2
9 * x^2 = 0
x = 0

Monotonie fallend
9 * x^2 < 0
x^2 < 0
keine Lösung

Monotonie steigend
9 * x^2 > 0
x^2 > 0
also stets, außer x = 0

Die Funktion ist stets steigend außer
bei x = 0. Dort ist die Funktion waagerecht.
( 0 | 0 ) ist ein Sattelpunkt.