Der Turmhelm der Kirche ist eine quadratische Pyramide. Wie viel Quadratmeter Dachfläche sind einzudecken?

Question

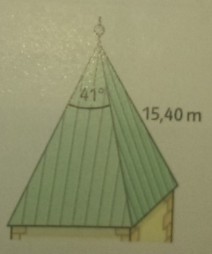
Aufgabe 7:

Der Turmhelm der Kirche ist eine quadratische Pyramide. Wie viel Quadratmeter Dachfläche sind einzudecken?

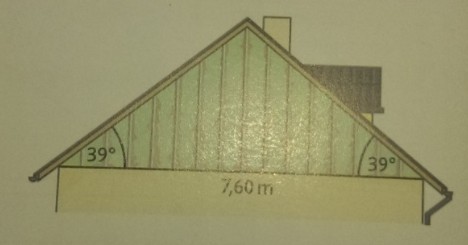
Aufgabe 8:

Welche Kosten entstehen, wenn die Holzverkleidung an der Giebelwand gestrichen wird? 11 Farbe reicht für \( 5 \mathrm{~m}^{2} \) und kostet 10,05 €.

Comments

Zu 8: beachte https://www.mathelounge.de/46535/flacheninhalt-dreieck-berechnen dort wurde das schon gelöst.

---

Zu 7. Das weiss ich schon. Du erkennst dort, dass du 4 Dreiecksflächen addieren musst.

Zeichne eines der Dreiecke auf und berechne die Teile, die du brauchst um seine Fläche zu bestimmen.

Answer 1

 Ich hoffe es kann dire für 8 weiter helfen.... 7,34 €

Comments

7,34 € Gesamte Kosten ;)

---

Beim Wurzelziehen ist etwas schiefgelaufen.

Berechne h direkt über den Tangens.

h / 3.8 = tan(39°)

h = 3.8 * tan(39°)   Einheit Meter.

Vgl. https://www.mathelounge.de/46535/flacheninhalt-dreieck-berechnen

---

Die Fläche ist falsch weil der Rechenweg falsch ist, und die Kosten sind als Folgefehler auch falsch.

---

UPS Sorry da muss es h=sqrt(x² - (c/2)²) sein :/

Answer 2

Hallo ahmed gustav,

zu 7)

  

        s = 15,40 m   ;   w = 20,5°

       sin(w) = (a/2) / s  →    a/2  = sin(w) * s    [ = Länge von BH ]

       h_a  mit Pythagoras  (oder cos(w))

       Gesucht ist die Mantelfläche  (4 Seitendreiecke)

        A_ΔBCE  =  1/2 * a * h_a

Gruß Wolfgang

Answer 3

Zu 8: kennst du die Formel für die Fläche eines Dreiecks? Die Höhe des Giebeldreiecks ist tan 39° * 3,8 m

Comments

Ja danke  hat mir geholfen ich weiß wie  ich berechnen soll :)

---

So geht es einfacher als mit dem weiter oben angegebenen Umweg über die Berechnung zuerst der Sachschräge mit dem Cosinus und dann der Giebelhöhe mit Pythagoras.

---

So geht es einfacher als mit dem weiter oben angegebenen Umweg über die Berechnung zuerst der Dachschräge mit dem Cosinus und dann der Giebelhöhe mit Pythagoras.