Hallo Valeria,
Willkommen in der Mathelounge!
Nochmal zur Klarstellung, welcher Winkel mit \(\gamma\) gemeint ist. Ich fragte:
... oder der Winkel in der Spitze einer dreieckigen Seitenfläche
Du antwortestes:
Der Winkel ist oben in der Spitze
Ich gehe also davon aus, dass der hier blau markierte WInkel gemeint ist
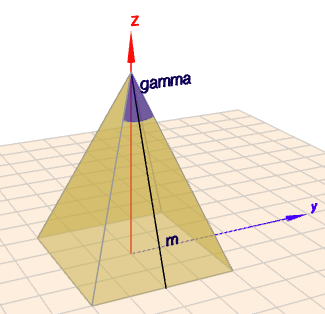
Einmal den Pythagoras und einmal den Tangens vom halben WInkel. Ist \(m\) die Höhe einer Seitenfläche, \(a\) die Kante der quadratischen Grundfläche und \(h\) die Höhe der Pyramide, so ist$$m = \sqrt{h^2 + \left(\frac a2\right)^2}$$Weiter ist \(m\) die Ankathete und \(a/2\) die Gegenkathete für \(\gamma/2\) im rechtwinkligen Dreieck . Folglich ist$$\tan\left(\frac\gamma2\right) = \frac{a}{2m} = \frac{a}{2\sqrt{h^2 + \left(\frac a2\right)^2}}$$So und dies gilt es nun nach \(a\) aufzulösen:$$\begin{aligned}\tan\left(\frac\gamma2\right) &= \frac{a}{2\sqrt{h^2 + \left(\frac a2\right)^2}} \\2\tan\left(\frac\gamma2\right) \sqrt{h^2 + \left(\frac a2\right)^2} &= a &&|\,^2\\4\tan^2\left(\frac\gamma2\right)\left(h^2 + \left(\frac a2\right)^2\right) &= a^2 \\4\tan^2\left(\frac\gamma2\right)h^2 + 4\tan^2\left(\frac\gamma2\right)\left(\frac a2\right)^2 &= a^2 \\4\tan^2\left(\frac\gamma2\right)h^2 + \tan^2\left(\frac\gamma2\right)a^2 &= a^2 &&|\,-\tan^2\left(\frac\gamma2\right)a^2\\4\tan^2\left(\frac\gamma2\right)h^2 &= a^2 -\tan^2\left(\frac\gamma2\right)a^2\\4\tan^2\left(\frac\gamma2\right)h^2 &= a^2\left(1 -\tan^2\left(\frac\gamma2\right)\right)&&|\,\div \left(1 -\tan^2\left(\frac\gamma2\right)\right)\\\frac{4\tan^2\left(\frac\gamma2\right)h^2}{1 -\tan^2\left(\frac\gamma2\right)} &= a^2 &&|\,\sqrt{}\\a &= \frac{2\tan\left(\frac\gamma2\right)h}{\sqrt{1 -\tan^2\left(\frac\gamma2\right)}}\end{aligned}$$da hast Du Deine 'Formel'
Tipp: die Frage nach der Formel ist immer die falsche Frage. Es ist besser nach Zusammenhängen und Abhängigkeiten zu suchen. Was hängt mit was zusammen?
Gruß Werner