Integral Seespiegel berechnen

Question

Brauche eure Hilfe bei folgender Aufgabenstellung:

y=0 sei gewachsenes Terrain und y= (x^2 / 2) +  x - 6 der Querschnitt eines Flussbettes.

Die Querschnittsfläche des Wassers im Fluss beträgt 30m^2

Die Frage lautet:

Wie viel liegt der Seespiegel unterhalb des gewachsenen Terrains?

Danke für eure Hilfe

Comments

Einmal ist es der Seespiegel und einmal die Flussoberfläche. Warum?

Answer 1

Schneide die Gerade mit der Gleichung y = a mit der Parabel mit der Gleichung y= (x² / 2) +  x - 6. Bestimme dann das Integral in den Grenzen der beiden Schnittpunkte. Wenn du diesen Term gleich 30 setzt, erhältst du a. Der Betrag von a gibt an, wie viele Meter der Seespiegel unterhalb des gewachsenen Terrains liegt.

Comments

Danke für dein Tipp.

Könntest du mir noch helfen wie ich die:

Die Horizontaldistanz der Flussufer zur tiefsten Stelle im Fluss und wie tief das Wasser an der tiefsten Stelle im Fluss berechnet werden kann?

Vielen Dank

---

Die Horizontaldistanz der Flussufer zur tiefsten Stelle im Fluss

Die Fussufer sind die Nullsellen der Parabel. Ihr halber Abstand ist die Horizontaldistanz der Flussufer zur tiefsten Stelle im Fluss

und wie tief das Wasser an der tiefsten Stelle im Fluss berechnet werden kann?

Die tieftste Stelle ist der Scheitelpunkt der Parabel. Seine y-Koordinate nennt die Tiefe des Wassers an der tiefsten Stelle.

---

Salü Roland

und wie tief das Wasser an der tiefsten Stelle im Fluss berechnet werden kann?

f(x) = 1/2·x² + x - 6

a = 1/2       b = 1       c = -6

Koordinaten des Scheitelpunkts:

x  = -b/(2a) = (-1)/(2·(1/2)) = -1
 s

y  = c - b²/(4a) = -6 - 1/(4·(1/2)) = -13/2
 s

Scheitelpunktform der Funktionsgleichung:

f(x) = 1/2·(x + 1)² - 13/2


Schnittpunkte mit den Koordinatenachsen:

 • Nullstellen (Schnittpunkte mit x-Achse):

      x  = -1 - sqr(13) = -4,6055512755...
       1

      x  = -1 + sqr(13) = 2,6055512755...
       2

 • Schnittpunkt mit y-Achse bei y = f(0) = c = -6

Die Horizontaldistanz der Flussufer zur tiefsten Stelle im Fluss

                ___________                        ___________
          p     |  p²      |                p     |  p²       |
  x  = - ——— -  | ——— - q           x  = - ——— +  | ——— - q
   1      2    \|  4                 2      2    \|  4

  x  = -2/2 - sqr( 2²/4 + 12 )
   1 
     = -1 - sqr( 1 + 12 )

     = -1 - sqr(13)

     = -1 - 3,605551275463989

     = -4,605551275463989


  x  = -2/2 + sqr( 2²/4 + 12 )
   2 
     = -1 + sqr( 1 + 12 )

     = -1 + sqr(13)

     = -1 + 3,605551275463989

     = 2,605551275463989

Stimmt das so, oder habe ich da was falsch verstanden?

Danke dir....

Hier komme ich nicht auf ein Resultat wo plausibel sein könnte...

Schneide die Gerade mit der Gleichung y = a mit der Parabel mit der Gleichung y= (x² / 2) +  x - 6. Bestimme dann das Integral in den Grenzen der beiden Schnittpunkte. Wenn du diesen Term gleich 30 setzt, erhältst du a. Der Betrag von a gibt an, wie viele Meter der Seespiegel unterhalb des gewachsenen Terrains liegt.

Kannst du mir da weiterhelfen?

Habe mal so angefangen:

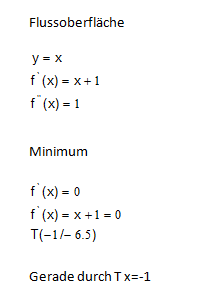
Weiter komme ich irgendwie nicht mehr...

---

Sorry hat es mir nicht reinkopiert:

---

Seine y-Koordinate nennt die Tiefe des Wassers an der tiefsten Stelle.

Das ist mit Sicherheit falsch und der Rest nur dann richtig, wenn  "Fluss" = "Flussbett"  ist.

---

Liebe Claudia, am Anfang deiner langen Ausführungen fehlt die Angabe der Tiefe an der tiefsten Stelle, die du als y-Koordinate des Scheitelpunktes mit 13/2 m richtig angegeben hattest.

Als Horizontaldistanz zwischen den Nullstellenx₁=-1-√13 und x₂=-1+√13 kommt 2·√13 heraus. Davon die Hälfte ist die Horizotaldistanz Ufer/tiefste Stelle, nämlich √13≈3,6.

Die Schnittstellen von y=-a mit y= (x² / 2) +  x - 6 sind x_1/2=-1±√(13-2a). Das sind die Integrationsgrenzen.Das Unbestimmte Integral ist x³/6+x²/2-6x. Hier werden die Grenzen eingesetzt (obere Grenze eingesetzt minus untere Grenze eingesetzt). Wenn du das Ergebnis  -30 (Fläche unterhalb der x-Achse) setzt, erhältst du nach längerer Rechnung a=2. Der Wasserspiegel liegt also 2m unterhalb der Erdoberfläche.

---

Das Unbestimmte Integral ist x³/6+x²/2-6x.

Das ist es allerdings nicht.

---

Vielen Dank Roland

Die beiden oberen verstehe ich nun.

Habe aber immer noch Mühe das hier zu verstehen:

"Die Schnittstellen von y=-a mit y= (x² / 2) +  x - 6 sind x_1/2=-1±√(13-2a). Das sind die Integrationsgrenzen.Das Unbestimmte Integral ist x³/6+x²/2-6x. Hier werden die Grenzen eingesetzt (obere Grenze eingesetzt minus untere Grenze eingesetzt). Wenn du das Ergebnis  -30 (Fläche unterhalb der x-Achse) setzt, erhältst du nach längerer Rechnung a=2. Der Wasserspiegel liegt also 2m unterhalb der Erdoberfläche."

Könntest du mir dies einwenig genauer machen?

Hast was von einer längeren Rechnung geschrieben, aber auf die komme ich nicht...

Bin nicht so ein Mathematik Ass, sorry...

---

Ich werde dir die Integrationsgrenzen vorrechnen. Vorweg nur soviel: mit 30 m² ist eine Fläche gegeben, die zwischen den Graphen von y=-a und y= (x² / 2) +  x - 6 liegt. Hier braucht man zunächst die beiden Schnittpunkte der Graphen. Die erhält man durch Gleichsetzen: -a= (x² / 2) +  x - 6.Um die pq-Formel anwenden zu können, muss ich etwas umformen: x²+2x-12+2a=0. Dann ist p=2 und  q=2a-12. also x_1/2=-1±√(1-2a+12) oder x_1/2=-1±√(13-2a).

Jetzt ist die Differenzfunktion d(x) zu bilden (das hatte ich bisher vergessen): d(x)= (x² / 2) +  x - 6+a.

Deren Stammfunktion ist x³/6+x²/2-(6-a)x. Hier müssen nun die Integrationsgrenzen x₁=-1-√(13-2a) (untere Grenze) und x₂=-1+√(13-2a) (obere Grenze) eingesetzt werden (obere Grenze einsetzen minus untere Grenze einsetzen). Das Ergebnis soll gleich 30 sein. Auf diese Weise ergibt sich eine Bestimmungsgleichung für a, die dann nach a aufgelöst werden muss. Das erspare ich dir, weil ich fürchten muss dass das zu kompliziert wird. Mein Ergebnis war (glaube ich) falsch.

Answer 2

Stimmen deine Angaben ?

Der Querschnitt des Flußbetts ergibt sich bei mir
zu 18.58 m^2.

f ( x ) = 1/2 * x^2 + x - 6
Nullstellen
± 2.61 m

Stammfunktion
F ( x ) = 1/6 * x^3 + 1/2*x^2 - 6*x
[ F ( x ) ] zwischen - 2.61 und + 2.61 = 18.58 m^2

Eine Wasserfläche von 30 m^2 passt also
nicht ins Flußbett.

mfg Georg

Comments

Korrektur :
die Fuinktion ist keine zur y-Achse symmetrische
Funktion.
Die Nullstellen sind
- 4.61 und 2.51

F ( x ) = 1/6 * x³ + 1/2*x² - 6*x
[ F ( x ) ] zwischen - 4.61 und + 2.61 = 62.50 m²

---

Das ist die komplette Aufgabe wo ich erhalten habe.

Gruss

---

Hallo Claudia,
Die Nullstellen der Funktion
x = - 4.61 und x = 2.51 stimmen ja in unser
beiden Rechnungen überein.
Die " Horizontaldiastanz " dürfte wohl der Abstand sein
Abstand = 2.505 + 4.605 = 7.11 m

Scheitelpunktform
f ( x ) = 1/2 * ( x + 1) ^2 - 6.5

Geht noch weiter.

---

Die ganze Angelegenheit erscheint mir
tierisch kompliziert.
Aus Vereinfachungsgründen habe ich die
Funktion mittig zur y-Achse verschoben
und dann noch 6.5 Einheiten noch oben.
Sprich : in den Ursprung des Koordinatensystems


Die Funktion lautet dann f ( x ) = 1/2 * x^2

für y = 6.5 ist x = ± 3.605

Ffläche = 7.21 * 6.5 minus 1/6 * x^3 zwischen -3.605 und 3.605
Fläche = 31.25 m^2

mfg Georg

geht noch weiter

ich komme aus dem Korrigieren auch gar nicht mehr raus

Korrektur :
die Fuinktion ist keine zur y-Achse symmetrische
Funktion.
Die Nullstellen sind
- 4.61 und 2.61

F ( x ) = 1/6 * x³ + 1/2*x² - 6*x
[ F ( x ) ] zwischen - 4.61 und + 2.61 = 31.25 m²

Dann stimmen die beiden Funktionen wieder überein.

---

Hier meine Berechnung ( mit CAS )



t = 6.326 m