zu (b) Folgende Skizze zeigt die drei Dreiecke \(A'B'D\) (grün), \(B'D'C\) (rosa) und \(A'DB\) (gelb). Die Seite des äußeren Fünfecks sei \(s'=A'B'\) und und seine Diagonale \(d'=B'D'\). Die Seite des inneren Fünfecks sei \(s=AB\) und seine Diagonale \(d=BD\).
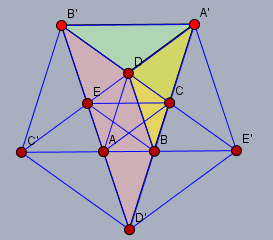
Ich behaupte ohne Beweis, dass alle drei ähnlich und die beiden kleineren auch konkruent sind. Die Dreiecke sind auch gleichschenklig. (siehe auch diese Antwort)
Daraus folgt auch, dass die Diagonale \(d=BD=B'D\) ist. Demnach ist $$d'=s+2d$$ Aus dem Verhältnis Basis zu Schenkel von grün und rosa folgt $$\frac{s'}{d}=\frac{d'}{d'-d} \space \Rightarrow \frac{s'}{d'}=\frac{d}{d'-d}$$ Weiter muss sein $$\frac{s'}{d'}=\frac{s}{d}$$ Der Vergleich der letzten beiden Gleichungen plus Einsetzen der ersten in das Ergebnis ergibt
$$\frac{s}{d}=\frac{d}{s+2d-d} \space \Rightarrow \frac{d}{s}=\frac{s}{d}+1 \space \Rightarrow \left( \frac{d}{s}\right)^2=\frac{d}{s}+1$$
Mit \(s=1\) erhält man den Term aus der Aufgabenstellung.
zu (c) Man kann zeigen, dass \(d\) nicht rational ist, wenn man die Parität von \(p\) und \(q\) betrachtet. \(p\) und \(q\) seihen zwei teilerfremde Zahlen. Wenn sie nicht teilerfremd wären, so könnte man kürzen, bis sie teilerfremd sind - ich schränke also nichts ein. Dann wäre
$$\left( \frac{p}{q} \right)^2 = \frac{p}{q} + 1 \space \Rightarrow p^2=pq + q^2$$
Beide Zahlen dürfen nicht beide ungerade sein, da sonst rechts die Summe gerade und links das Produkt ungerade ist. \(p\) kann auch nicht gerade sein und \(q\) ungerade, da sonst links eine gerade Zahl steht und rechts eine ungerade. Und umgekehrt geht es auch nicht auf, da dann links eine ungerade Zahl steht und rechts die Summe aus zwei geraden Zahlen. Also bleibt nur, dass \(p\) und \(q\) gerade sein müssen - das wiederum ist ein Widerspruch zu der Annahme, dass beide teilerfremd sind.
Daraus folgt, dass es keine zwei ganzen Zahlen \(p\) und \(q\) gibt, die diese Gleichung erfüllen.
q.e.d.